Cho hình chóp S.ABC có $\large SA\perp (ABC),\widehat{BAC}=12
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có SA⊥(ABC),^BAC=120∘,AB=AC=a và SA=a2√3. Tính góc tạo bởi hai mặt phẳng (SBC) và (ABC).
Đáp án án đúng là: C
Lời giải chi tiết:
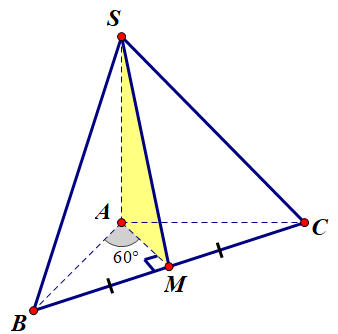
Gọi M là trung điểm của BC⇒AM⊥BC⇒(^(SBC),(ABC))=^SMA.
Tam giác ABC cân tại A nên:
AM=AB⋅cos^MAB=a⋅cos60∘=a2
Trong tam giác vuông SAM có:
tan^SMA=SAAM=a2√3:a2=1√3⇒^SMA=30∘
Vậy (^(SBC);(ABC))=30∘
Đáp án C
Xem thêm các bài tiếp theo bên dưới