Cho hình chóp đều $\large S.ABC$ có cạnh đáy bằng $\large a$, cạnh bên

Cho hình chóp đều $\large S.ABC$ có cạnh đáy bằng $\large a$, cạnh bên gấp hai lần cạnh đáy. Thể tích của khối chóp đã cho bằng:

• A.

  A. $\large\frac{\sqrt{11}a^{3}}{4}$

• B.

  B. $\large\frac{\sqrt{11}a^{3}}{6}$

• C.

  C. $\large\frac{\sqrt{11}a^{3}}{12}$

• D.

  D. $\large\frac{\sqrt{13}a^{3}}{12}$

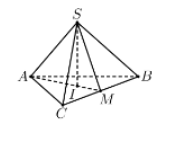
Gọi $\large I$ là tâm đường tròn ngoại tiếp tam giác $\large ABC$. Vì $\large S.ABC$ là khối chóp đều nên suy ra $\large SI\perp (ABC)$

Gọi $\large M$ là trung điểm của $\large BC\Rightarrow AI=\frac{2}{3}AM=\frac{a\sqrt{3}}{3}$

Tam giác $\large SAI$ vuông tại $\large I$, có:

$\large SI=\sqrt{SA^{2}-AI^{2}}=\sqrt{(2a)^{2}-\left ( \frac{a\sqrt{3}}{3} \right )^{2}}=\frac{a\sqrt{33}}{3}$

Diện tích tam giác $\large S_{\bigtriangleup ABC}=\frac{a^{3}\sqrt{3}}{4}$

Vậy thể tích của khối chóp: $\large V_{S.ABC}=\frac{1}{3}S_{\bigtriangleup ABC}.SI=\frac{\sqrt{11}a^{3}}{12}$

Đáp án C