Cho hình chóp $\Large S.ABC$ có $\Large SA$ vuông góc với mặt phẳng $\

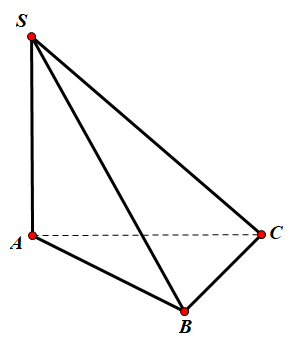
Cho hình chóp $\Large S.ABC$ có $\Large SA$ vuông góc với mặt phẳng $\Large (ABC),$ đáy là tam giác đều, $\Large SA=\dfrac{3a}{2},$ $\Large AB=a$ (tham khảo hình bên). Tính góc giữa hai mặt phẳng $\Large (SBC)$ và $\Large (ABC).$

• A. $\Large 30^{\circ}.$
• B. $\Large 45^{\circ}.$
• C. $\Large 60^{\circ}.$
• D. $\Large 90^{\circ}.$

Chọn C

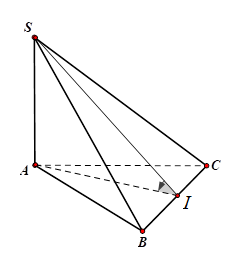
Ta có: $\Large (SBC)\cap (ABC)=BC \ (1)$
Gọi I là trung điểm của BC. Suy ra $\Large AI \perp BC \ (2)$
Ta có: $\Large \left\{\begin{align} & AI \perp BC \\ & BC \perp SA \end{align}\right.$ $\Large \Rightarrow BC \perp SI \ (3)$
Từ (1), (2), (3) suy ra góc giữa hai mặt phẳng (SBC) và (ABC) là góc giữa hai đường thẳng SI và AI.

Xét tam giác vuông SAI có $\Large SA=\dfrac{3a}{2}, AI=\dfrac{a\sqrt{3}}{2}$
Suy ra $\Large \tan \widehat{SIA}=\dfrac{SA}{AI}=\dfrac{\dfrac{3a}{2}}{\dfrac{a\sqrt{3}}{2}}=\sqrt{3}$

Vậy góc giữa hai mặt phẳng (SBC) và (ABC) bằng $\Large 60^{\circ}.$