Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm

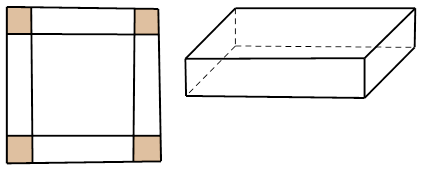
Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $\Large x$ (cm), rồi gập tấm nhôm lại để được một cái hộp không nắp (tham khảo hình vẽ bên). Tìm $\Large x$ để hộp nhận được có thể tích lớn nhất (giả thiết bề dày tấm tôn không đáng kể).

 

• A.

  $\Large x=2.$

• B.

  $\Large x=3.$

• C.

  $\Large x=4.$

• D.

  $\Large x=6.$

Chọn A

Hình hộp có đáy là hình vuông cạnh bằng $\Large 12-2x,$ chiều cao bằng $\Large x.$

Điều kiện $\Large 0 < x < 6$

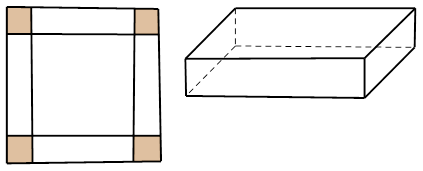
Thể tích khối hộp là: $\Large V=(12-2x)^2.x=4(6-x)^2.x.$

Áp dụng bất đẳng thức Cauchy cho 3 số dương $\Large \sqrt[3]{(6-x)(6-x).2x} \leq \dfrac{(6-x)+(6-x)+2x}{3}$

$\Large \Leftrightarrow (6-x)(6-x).2x \leq 4^3 \Leftrightarrow 4(6-x)^2.x \leq 2.4^3 \Leftrightarrow V \leq 128$ (hằng số).

Dấu "=" xảy ra $\Large \Leftrightarrow 6-x=2x \Leftrightarrow x=2.$

Vậy thể tích khối hộp lớn nhất khi $\Large x=2.$