Cho hàm số $\Large f(x)$ có đạo hàm $\Large {f}'(x)=x(x^2-1)^2(x^2-4)^

Cho hàm số $\Large f(x)$ có đạo hàm $\Large {f}'(x)=x(x^2-1)^2(x^2-4)^3.$ Số điểm cực tiểu của hàm số $\Large f(x)$ là

• A. 3.
• B. 2.
• C. 1.
• D. 5.

Chọn B

$\Large {f}'(x)=x(x^2-1)^2(x^2-4)^3=x(x-1)^2(x+1)^2(x-2)^3(x+2)^3.$

$\Large {f}'(x)=0$ $\Large \Leftrightarrow \left[\begin{align} & x=0 \\ & x=\pm 1 \\ & x=\pm 2 \end{align}\right.$

Ta có bảng xét dấu $\Large {f}'(x):$

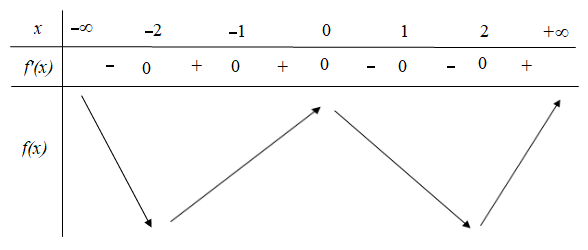
Vậy số điểm cực tiểu của hàm số $\Large f(x)$ là 2.