Cho hình chóp $\Large S.ABC$ có $\Large SA$ vuông góc với mặt phẳng $

Cho hình chóp $\Large S.ABC$ có $\Large SA$ vuông góc với mặt phẳng $\Large (ABC)$, $\Large SA=a\sqrt{3}$, tam giác $\Large ABC$ vuông tại $\Large B$ và $\Large AC=2a$, $\Large \widehat{ACB}=30^{\circ}$ (minh họa như hình bên). Góc giữa đường thẳng $\Large SB$ và mặt phẳng $\Large (ABC)$ bằng

• A.

  $\Large 30^{\circ}$.

• B.

  $\Large 45^{\circ}$.

• C.

  $\Large 90^{\circ}$.

• D.

  $\Large 60^{\circ}$.

Chọn D

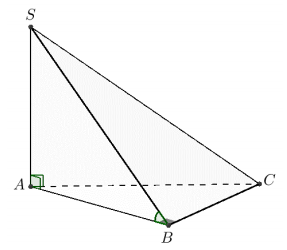
$\Large SA\perp (ABCD)$ $\Large \Rightarrow AB$ là hình chiếu vuông góc của $\Large SB$ trên mặt phẳng $\Large (ABC)$.

$\Large \Rightarrow \widehat{\big(SB, (ABC)\big)}=\widehat{(SB, AB)}=\widehat{SBA}$.

Xét tam giác $\Large ABC$ vuông tại $\Large B$, ta có: $\Large AB=AC.sin\widehat{ACB}=a$.

Xét tam giác $\Large SAB$ vuông tại $\Large A$, ta có: $\Large tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{3}\Rightarrow \widehat{SBA}=60^{\circ}$.