Cho hình chóp $\Large S.ABC$ có đáy là tam giác $\Large ABC$ vuông tại

Cho hình chóp $\Large S.ABC$ có đáy là tam giác $\Large ABC$ vuông tại $\Large B$, $\Large AB=BC=2a$, $\Large (SAB)\perp (ABC)$, $\Large (SAC)\perp (ABC)$. Gọi $\Large M$ là trung điểm $\Large AB$, mặt phẳng $\Large (\alpha)$ qua $\Large SM$ và $\Large (\alpha)$ song song $\Large BC$ cắt $\Large AC$ tại $\Large N$, góc giữa hai mặt phẳng $\Large (SBC)$ và $\Large (ABC)$ bằng $\Large 60^{\circ}$. Tính theo $\Large a$ khoảng cách giữa hai đường thẳng $\Large AB$ và $\Large SN$.

• A.

  $\Large \dfrac{2a\sqrt{156}}{13}$.

• B.

  $\Large \dfrac{a\sqrt{13}}{156}$.

• C.

  $\Large \dfrac{a\sqrt{156}}{13}$.

• D.

  $\Large \dfrac{a\sqrt{13}}{13}$.

Chọn C

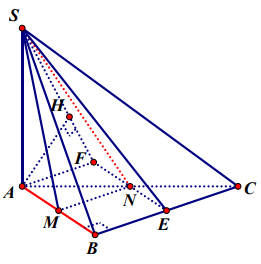
+ Ta có $\Large \left\{\begin{align} & (SAB)\perp (ABC) \\ & (SAC)\perp (ABC) \\ & (SAB)\cap (SAC)=SA \end{align}\right.$ $\Large \Rightarrow SA\perp (ABC)$.

+ $\Large \left\{\begin{align} & SA\perp (ABC)\Rightarrow SA\perp BC \\ & BC\perp BA \end{align}\right.$ $\Large \Rightarrow BC\perp (SAB)$.

+ $\Large \left\{\begin{align} & (SBC)\cap (ABC)=BC \\ & AB\perp BC, AB\subset (ABC) \\ & SB\perp BC, SB\subset (SBC) \end{align}\right.$ $\Large \Rightarrow$ góc giữa hai mặt phẳng $\Large (SBC)$ và $\Large (ABC)$ là $\Large (SB, AB)\Rightarrow SBA=60^{\circ}$. Suy ra $\Large SA=tan60^{\circ}.2a=2a\sqrt{3}$.

+ Trong mặt phẳng $\Large (ABC)$, qua $\Large N$, kẻ đường thẳng song song với $\Large AB$ cắt $\Large BC$ tại $\Large E$, kẻ đường thẳng qua $\Large A$ song song với $\Large BC$, cắt $\Large NE$, tại $\Large F$. Khi đó $\Large ABEF$ là hình chữ nhật.

+ Ta có $\Large \left\{\begin{align} & AB// EF\Rightarrow AB// (SEF) \\ & SN\subset (SEF) \end{align}\right.$ $\Large \Rightarrow d(AB, SN)=d\big(AB, (SEF)\big)=d\big(A, (SEF)\big)$.

+ Vì $\Large ABEF$ là hình chữ nhật nên $\Large (SAF)\perp (SEF)$, trong mặt phẳng $\Large (SAF)$, kẻ $\Large AH\perp SF$, $\Large H\in SF$ $\Large \Rightarrow d\big(A, (SEF)\big)=AH$.

+ Ta có $\Large AF=BE=a$ $\Large \Rightarrow AH=\dfrac{AS.AF}{\sqrt{AS^2+AF^2}}$ $\Large =\dfrac{2a\sqrt{3}a}{\sqrt{12a^2+a^2}}=\dfrac{a\sqrt{156}}{13}$.