Cho hàm số $\Large y=f(x)$ liên tục trên $\Large \mathbb{R}$ có đồ thị

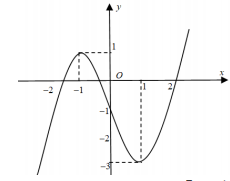
Cho hàm số $\Large y=f(x)$ liên tục trên $\Large \mathbb{R}$ có đồ thị như hình vẽ

Phương trình $\Large f(cosx)=m$ có ít nhất một nghiệm thuộc $\Large \left[\dfrac{\pi}{2}; \pi \right)$ khi và chỉ khi

 

• A.

  $\Large m\in [-3; -1)$.

• B.

  $\Large m\in [-1; 1]$.

• C.

  $\Large m\in (-1; 1]$.

• D.

  $\Large m\in [-1; 1)$.

Chọn D

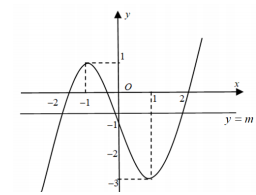
Ta có: số nghiệm của phương trình $\Large f(cosx)=m$ là số giao điểm của đồ thị hàm số $\Large y=f(cosx)$ và đường thẳng $\Large y=m$.

Phương trình $\Large f(cosx)=m$ có ít nhất một nghiệm $\Large x\in \left[\dfrac{\pi}{2}; \pi \right)$ thì $\Large cosx\in (-1; 0]$ $\Large \Leftrightarrow f(cosx)\in [-1; 1)$ $\Large \Leftrightarrow m\in [-1; 1)$.