Cho hàm số $\Large y=f(x)$. Đồ thị của hàm số $\Large y={f}'(x)$ như h

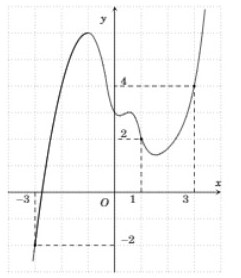
Cho hàm số $\Large y=f(x)$. Đồ thị của hàm số $\Large y={f}'(x)$ như hình sau. Đặt $\Large g(x)-2f(x)-{{(x+1)}^{2}}$. Mệnh đề nào sau đây là mệnh đề đúng ?

• A.

  A. $\Large g(-1)>g(-3)>g(3)$

• B.

  B. $\Large g(-3)>g(3)>g(1)$

• C.

  C. $\Large g(3)>g(-3)>g(1)$

• D.

  D. $\Large g(1)>g(3)>g(-3)$

Ta có ${g}'(x)=2{f}'(x)-2(x+1)$

$\Rightarrow {g}'(x)=0\Leftrightarrow {f}'(x)=x+1$

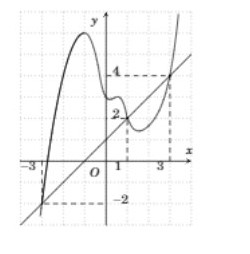
Từ đồ thị hàm số ta thấy đường thẳng $y=x+1$ cắt đồ thị $y={f}'(x)$ tại 3 điểm $A(-3;-2),B(1;2),C(3;4)$

Suy ra ${g}'(-3)={g}'(1)={g}'(3)=0$ và $g(x)$ có bảng biến thiên như sau :

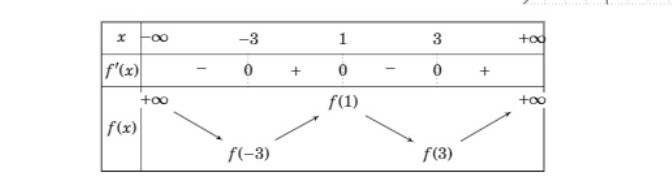
Từ đó suy ra $g(1)$ là số lớn nhất trong ba số $g(-3),g(1),g(3)$ (1)

Từ đồ thị hàm số ta thấy diện tích hình phẳng giới hạn bởi $y={f}'(x),y=x+1$ và $x=-3,x=1$ lớn hơn diện tích hình phẳng giới hạn bởi $y={f}'(x),y=x+1$ và $x=1,x=3$. Do đó 

$\int\limits_{-3}^{1}{\left[ {f}'(x)-(x+1) \right]dx>\int\limits_{1}^{3}{\left[ (x+1)-{f}'(x) \right]dx\Leftrightarrow \int\limits_{-3}^{1}{{g}'(x)dx>-\int\limits_{1}^{3}{{g}'(x)dx}}}}$

Suy ra $g(1)-g(-3)>g(1)-g(3)\Leftrightarrow g(3)>g(-3)$ (2)

Từ (1) và (2) ta có $g(1)>g(3)>g(-3)$

Chọn đáp án D