Cho hàm số y=f(x) có đạo hàm cấp hai trên R
Lưu về Facebook:
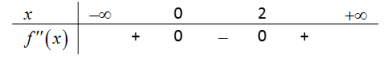
MỤC LỤC
Câu hỏi:
Cho hàm số y=f(x) có đạo hàm cấp hai trên R. Biết f′(0)=3, f′(2)=f′(−2018)=0, và bảng xét dấu của f′(x) như sau
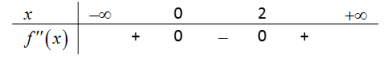
Hàm số y=f(|x−1|−2018) đạt giá trị nhỏ nhất tại x0 thuộc khoảng nào sau đây?
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
Từ bảng xét dấu của f″(x) và giả thiết f′(0)=3, f′(2)=f′(−2018)=0 suy ra bảng biến thiên của hàm số y=f′(x) như sau
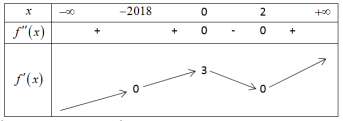
Từ đó suy ra bảng biến thiên của hàm số y=f(x):
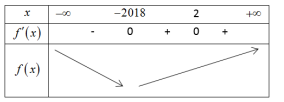
Hàm số y=f(|x−1|−2018) đạt giá trị nhỏ nhất khi và chỉ khi |x−1|−2018=−2018 ⇔|x−1|=0 ⇔x=1∈(−1009;2).