Cho hàm số y=2x−12x−2 có đồ thị (C). Gọi $
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hàm số y=2x−12x−2 có đồ thị (C). Gọi M(x0;y0) (với x0>1) là điểm thuộc (C), biết tiếp tuyến của (C) tại M cắt tiệm cận đứng và tiệm cận ngang lần lượt tại A và B sao cho SΔOHB=8SΔOIA (trong đó O là gốc tọa độ, I là giao điểm hai tiệm cận). Tính S=x0−4y0.
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
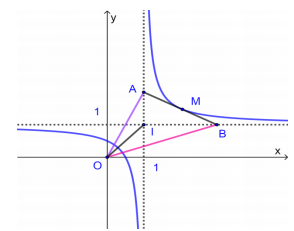
Ta có y=2x−12x−2=1+12x−2
TCĐ: x=1(d1), TCN: y=1(d2). Điểm I(1;1).
Ta có y′=−12(x−1)2
Giả sử M(x0;1+12x−2)∈(C)
Phương trình tiếp tuyến tại M là Δ:y=−12(x0−1)2(x−x0)+1+12x0−2
A=Δ∩d1 ⇒A(1;x0x0−1), B=Δ∩d2 ⇒B(2x0−1;1), →IB=(2x0−2;0); →IA=(0;1x0−1).
Ta có SΔOIB=8SΔOIA ⇔12.1.IB=8.12.1.IA ⇔IB=8IA
⇔|2x0−2|=8.|1x0−1| ⇔(x0−1)2=4 ⇔[x0=3(TM)x0=−1(L)
⇒y0=54 ⇒S=x0−4y0=3−4.54=−2.