Cho hàm số $\Large y=f(x)$ có bảng xét dấu đạo hàm như sau: Hàm số $\L
Lưu về Facebook:
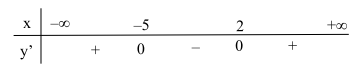
MỤC LỤC
Câu hỏi:
Cho hàm số $\Large y=f(x)$ có bảng xét dấu đạo hàm như sau:
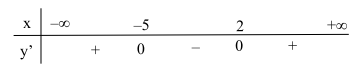
Hàm số $\Large g(x)=f(3-2^x)$ đồng biến trên khoảng nào sau đây:
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
Ta có $\Large {g}'(x)=-2^x\mathrm{ln}2.{f}'(3-2^x).$
Để $\Large g(x)=f(3-2^x)$ đồng biến thì
$\Large {g}'(x)=-2^x\mathrm{ln}2.{f}'(3-2^x) \geq 0 \Leftrightarrow {f}'(3-2^x) \leq 0 \Leftrightarrow -5 \leq 3-2^x \leq 2 \Leftrightarrow 0 \leq x \leq 3.$
Vậy hàm số đồng biến trên (1; 2).
Xem thêm các bài tiếp theo bên dưới
- Trong không gian Oxyz, cho hai đường thẳng $\Large d_1: \dfrac{x}{2}=\
- Cho $\Large a > 0, b > 0$ thỏa mãn $\Large \mathrm{log}_{4a+5b+1}(16a^
- Cho hàm số $\Large f(x)$ có đạo hàm liên tục trên $\Large \mathbb{R}.$
- Cho hình chóp S.ABC có SA vuông góc với đáy, đáy là tam giác đều, $\La
- Cho các số thực a, b, c, d thỏa mãn $\Large \mathrm{log}_{a^2+b^2+2}(4