Cho các số thực a, b, c, d thỏa mãn $\Large \mathrm{log}_{a^2+b^2+2}(4

Cho các số thực a, b, c, d thỏa mãn $\Large \mathrm{log}_{a^2+b^2+2}(4a+6b-7)=1$ và $\Large 27^c.81^d=6c+8d+1.$ Tìm giá trị nhỏ nhất của biểu thức $\Large P=(a-c)^2+(b-d)^2.$

• A.

  $\Large \dfrac{49}{25}.$

• B.

  $\Large \dfrac{64}{25}.$

• C.

  $\Large \dfrac{7}{5}.$

• D.

  $\Large \dfrac{8}{5}.$

Chọn A

Ta có $\Large \mathrm{log}_{a^2+b^2+2}(4a+6b-7)=1 \Leftrightarrow a^2+b^2+2=4a+6b-7 \Leftrightarrow (a-2)^2+(b-3)^2=4 \ (1).$

Lại có $\Large 27^c.81^d=6c+8d+1 \Leftrightarrow 3^{3c+4d}=2(3c+4d)+1 \ (2).$

Xét hàm số $\Large f(t)=3^t-2t-1$ trên $\Large \mathbb{R}.$

Khi đó $\Large f(t)$ là hàm số có đạo hàm liên tục trên $\Large \mathbb{R}$ và $\Large {f}'(t)=3^t.\mathrm{ln}3-2.$

Vì phương trình $\Large {f}'(t)=0$ có đúng một nghiệm $\Large \Bigg(t_0=\mathrm{log}_3\bigg(\dfrac{2}{\mathrm{ln}3}\bigg)\Bigg)$ nên phương trình $\Large f(t)=0$ có tối đa 2 nghiệm. Mặt khác, $\Large f(0)=f(1)=0$ nên $\Large S=\begin{Bmatrix} 0; 1 \end{Bmatrix}.$ là tập nghiệm của phương trình $\Large f(t)=0.$

Do đó, (2) tương đương với $\Large 3c+4d=0$ hoặc $\Large 3c+4d=1 \ (3).$

Trong mặt phẳng với hệ trục tọa độ Oxy, gọi điểm M có tọa độ (a; b) và điểm N có tọa độ (c; d). Khi đó, từ (1) suy ra M thuộc đường tròn tâm I (2; 3), bán kính $\Large r=2$ và từ (3) suy ra N thuộc đường thẳng $\Large \Delta_1: 3x+4y=0$ hoặc $\Large \Delta_2: 3x+4y-1=0.$

Ta cần tìm giá trị nhỏ nhất của biểu thức $\Large P=(a-c)^2+(b-d)^2=MN^2.$

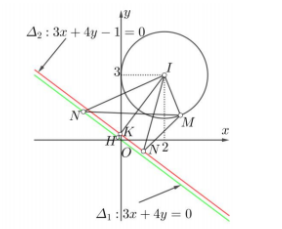
Gọi H, K lần lượt là hình chiếu vuông góc của I lên các đường thẳng $\Large \Delta_1$ và $\Large \Delta_2.$

Nếu N di chuyển trên đường thẳng $\Large \Delta_1$ thì $\Large MN \geq IN - IM \geq IH-r$ nên $\Large MN \geq \dfrac{8}{5}.$

Dấu đẳng thức xảy ra khi $\Large N\equiv H$ và M là giao điểm của đoạn thẳng IH với đường tròn. 

Nếu N di chuyển trên đường thẳng $\Large \Delta_2$ thì $\Large MN \geq IN - IM \geq IK-r$ nên $\Large MN \geq \dfrac{7}{5}.$

Dấu đẳng thức xảy ra khi $\Large N\equiv K$ và M là giao điểm của đoạn thẳng IK với đường tròn.

Từ hai trường hợp trên, ta có giá trị nhỏ nhất của MN bằng $\Large \dfrac{7}{5}.$ Từ đó, giá trị nhỏ nhất của biểu thức P bằng $\Large \dfrac{49}{25}.$