Cho hàm số $\Large f(x)=(x-1).(x-2)...(x-2020).$ Có bao nhiêu giá trị

Cho hàm số $\Large f(x)=(x-1).(x-2)...(x-2020).$ Có bao nhiêu giá trị nguyên của m thuộc đoạn [-2020; 2020] để phương trình $\Large {f}'(x)=m.f(x)$ có 2020 nghiệm phân biệt?

• A.

  2021.

• B.

  4040.

• C.

  4041.

• D.

  2020.

Chọn B

Ta có nhận xét: khi $\Large f(x)=0$ thì phương trình $\Large {f}'(x)=m.f(x)$ vô nghiệm.

Do đó: $\Large {f}'(x)=m.f(x) \Leftrightarrow m=\dfrac{{f}'(x)}{f(x)}.$

Xét hàm số $\Large g(x)=\dfrac{{f}'(x)}{f(x)}=\dfrac{1}{x-1}+\dfrac{1}{x+2}+\dfrac{1}{x-3}+...+\dfrac{1}{x-2020}.$

Ta có $\Large {g}'(x)=\dfrac{-1}{(x-1)^2}+\dfrac{-1}{(x-2)^2}+\dfrac{-1}{(x-3)^2}+...+\dfrac{-1}{(x-2020)^2} < 0$, $\Large \forall x \in \mathbb{R} \setminus \begin{Bmatrix}
1; 2; 3;...; 2020
\end{Bmatrix}$

Bảng biến thiên:

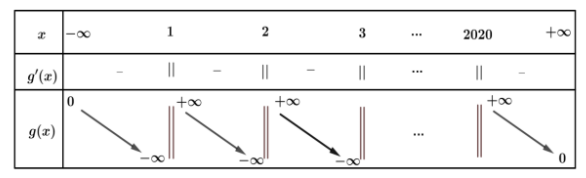
Dựa vào BBT, phương trình $\Large {f}'(x)=m.f(x)$ có 2020 nghiệm phân biệt khi và chỉ khi $\Large m > 0$ hoặc $\Large m < 0.$

Kết hợp với điều kiện m là số nguyên thuộc [-2020; 2020] nên

$\Large m \in \begin{Bmatrix} n \in \mathbb{Z}| -2020 \leq n \leq 2020, n \neq 0 \end{Bmatrix}.$

Vậy có tất cả 4040 giá trị m thỏa yêu cầu bài toán.