Cho hình chóp S.ABC có thể tích bằng 1. Mặt phẳng (Q) thay đổi song so

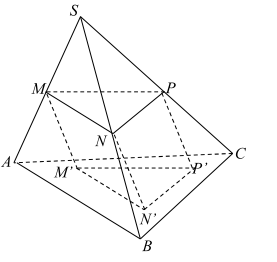
Cho hình chóp S.ABC có thể tích bằng 1. Mặt phẳng (Q) thay đổi song song với mặt phẳng (ABC) lần lượt cắt các cạnh SA, SB, SC tại M, N, P. Qua M, N, P kẻ các đường thẳng song song với nhau lần lượt cắt mặt phẳng (ABC) tại M', N', P'. Tính giá trị lớn nhất của thể tích khối lăng trụ MNP.M'N'P'.

• A.

  $\Large \dfrac{4}{9}.$

• B.

  $\Large \dfrac{1}{3}.$

• C.

  $\Large \dfrac{1}{2}.$

• D.

  $\Large \dfrac{8}{27}.$

Chọn A

Gọi $\Large \dfrac{SM}{SA}=x (0 < x < 1) \Rightarrow \dfrac{SN}{SB}=x=\dfrac{SP}{SC}$

$\Large \Rightarrow \dfrac{S_{\Delta MNP}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}NM.NP.sinMNP}{\dfrac{1}{2}BA.BC.sinABC}=\dfrac{NM}{BA}.\dfrac{NP}{BC}=x^2$

$\Large \Rightarrow S_{\Delta MNP}=x^2.S_{\Delta ABC}$

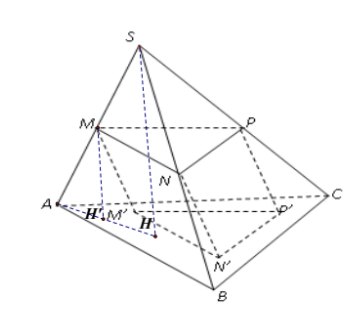
Gọi chiều cao của hình chóp SH, chiều cao của lăng trụ là MH':

$\Large \Rightarrow \dfrac{M{H}'}{SH}=\dfrac{AM}{AS}=1-x \Rightarrow M{H}'=(1-x)SH$

$\Large \Rightarrow V_{S.ABC}=\dfrac{1}{3}SH.S_{\Delta ABC}=1 \Leftrightarrow SH.S_{\Delta ABC}=3$

$\Large \Rightarrow V_{MNP.{M}'{N}'{P}'}$=$\Large M{H}'.S_{\Delta MNP}$=$\Large (1-x)SH.x^2.S_{\Delta ABC}$=$\Large x^2.(1-x).SH.S_{\Delta ABC}$=$\Large x^2.(1-x).3$

Xét hàm số: $\Large f(x)=3x^2-3x^3$ với $\Large x \in (0; 1)$

$\Large \Rightarrow {f}'(x)=6x-9x^2 \Rightarrow {f}'(x)=0$ $\Large \Leftrightarrow \left[\begin{align} & x=0 (loai) \\ & x=\dfrac{2}{3} \end{align}\right.$

Bảng biến thiên:

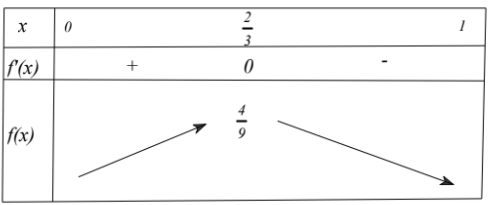
Vậy: $\Large max V_{MNP.{M}'{N}'{P}'}=\dfrac{4}{9}.$