Cho hàm số $\large y=ax^3+bx^2+cx+d$ có đồ thị như hình vẽ sau. Mệnh đ

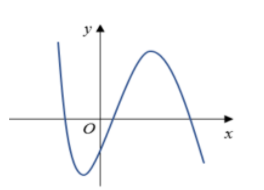
Cho hàm số $\large y=ax^3+bx^2+cx+d$ có đồ thị như hình vẽ sau. Mệnh đề nào sau đây là đúng?

 

• A. A. $\large a<0,b<0, c>0, d<0$
• B. B. $\large a<0, b>0, c<0, d<0$
• C. C. $\large a>0, b<0, c<0, d>0$
• D. D. $\large a<0, b>0, c>0, d<0$

Chọn D

Ta có: $\large y6=3ax^2+2bx+c; \,\, y''=6ax+2b$

Từ đồ thị ta thấy:

+ $\large \underset{x\to +\infty}{lim}\,\, y=-\infty$, suy ra $\large a<0$

+ $\large y(0)<0\Rightarrow d<0$ loại C

Đồ thị hàm số có hai điểm cực trị với hoành độ $\large x_1; x_2$ trái dấu và $\large x_1+x_2>0$. Ta suy ra phương trình $\large y'=0$ có hai nghiệm trái dấu và $\large x_1+x_2>0$

Ta suy ra: $\large x_1x_2=\dfrac{c}{3a}<0\Rightarrow c>0$ loại B

Hơn nữa, $\large \left\{\begin{align}& x_1+x_2=-\dfrac{b}{3a}>0$ $\large \Rightarrow b>0$ loại A