Cho hàm số $\Large y = f(x)$ có bảng biến thiên như sau Hàm số $\Large

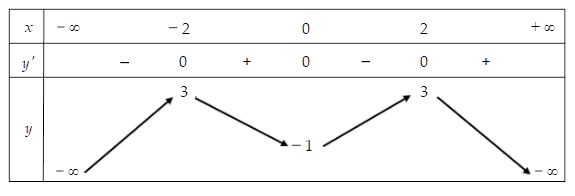
Cho hàm số $\Large y = f(x)$ có bảng biến thiên như sau

Hàm số $\Large y = f(x^{2} - 2)$ đồng biến trên khoảng nào

 

• A.

  A. $\Large (2; +\infty )$

• B.

  B. $\Large (0; 2 )$

• C.

  C. $\Large (-2; 0 )$

• D.

  D. $\Large (-\infty; -2 )$

Chọn A

Ta có:

$\Large y{}' = \left [ f(x^{2} - 2) \right ]{}' = 2xf{}'(x^{2} - 2)$

Khi đó:

$\Large y{}' = 0\Leftrightarrow \left[\begin{array}{l}x = 0 \\f{}' (x^{2}-2) = 0\\\end{array}\right.$

$\Large \Leftrightarrow \left[\begin{array}{l}x = 0 \\ x^{2} - 2 = -2 \\ x^{2} - 2 = 2 \\ x^{2} - 2 = 0\end{array}\right.\Leftrightarrow \left[\begin{array}{l}x = 0 \\ x = \pm 2 \\ x= \pm \sqrt{2}\end{array}\right.$.

Ta có bảng xét dấu của $\Large y{}' = \left [ f(x^{2} - 2) \right ]{}' $

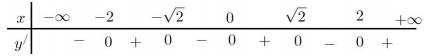
Vậy hàm số đồng biến trên $\Large \left ( -2; -\sqrt{2} \right )$ và $\Large \left ( 0; \sqrt{2} \right )$ và $\Large \left ( 2; +\infty  \right )$.