Cho hai số phức $\Large z_1, z_2$ thỏa mãn $\Large 2|z_1+5|=7$; $\Larg

Cho hai số phức $\Large z_1, z_2$ thỏa mãn $\Large 2|z_1+5|=7$; $\Large |z_2+1-3i|=|z_2-3-6i|$. Tính giá trị nhỏ nhất của biểu thức $\Large P=|z_1-z_2|$.

• A.

  $\Large \dfrac{5}{2}$.

• B.

  $\Large 4$.

• C.

  $\Large \dfrac{3}{2}$.

• D.

  $\Large 5$.

Chọn B

Ta có: $\Large 2|z_1+5|=7\Rightarrow |z_1+5|=\dfrac{7}{2}$.

Gọi $\Large M$ là điểm biểu diễn số phức $\Large z_1$.

Khi đó, $\Large M$ thuộc đường tròn tâm $\Large I(-5; 0)$ và bán kính $\Large R=\dfrac{7}{2}$.

Đặt $\Large z_2=x+yi$. Khi đó: $\Large |z_2+1-3i|=|z_2-3-6i|$

$\Large \Leftrightarrow |x+1+(y-3)i|=|x-3+(y-6)i|$

$\Large \Leftrightarrow \sqrt{(x+1)^2+(y-3)^2}=\sqrt{(x-3)^2+(y-6)^2}$

$\Large \Leftrightarrow (x+1)^2+(y-3)^2=(x-3)^2+(y-6)^2$

$\Large \Leftrightarrow y=\dfrac{35-8x}{6}$

Gọi $\Large N$ là điểm biểu diễn số phức $\Large z_2$. Khi đó $\Large N$ thuộc đường thẳng $\Large (d): y=\dfrac{35-8x}{6}$.

Ta có: $\Large P=|z_1-z_2|$ $\Large \Leftrightarrow P=MN$. Yêu cầu đề bài tương đương tìm giá trị nhỏ nhất độ dài của đoạn thẳng $\Large MN$.

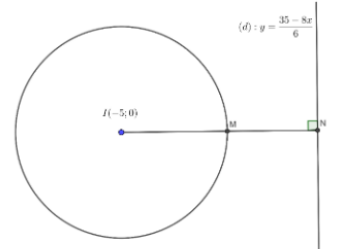
Bằng cách vẽ hình biểu diễn của $\Large M$, $\Large N$, ta xác định được giá trị nhỏ nhất độ dài của đoạn thẳng $\Large MN$ như hình vẽ trên.

Suy ra $\Large MN_{\min}=d_{\left(I, (d)\right)}-IM=IN-R$

• $\Large N\in (d)\Rightarrow N\left(x; \dfrac{35-8x}{6}\right)$ $\Large \Rightarrow \overrightarrow{IN}\left(x+5; \dfrac{35-8x}{6}\right)$

$\Large \overrightarrow{u_d}\left(1; \dfrac{-8}{6}\right)\perp \overrightarrow{IN}$ $\Large \Rightarrow \overrightarrow{IN}.\overrightarrow{u_d}=0$ $\Large \Rightarrow x+5-\dfrac{8}{6}.\dfrac{35-8x}{6}=0$

$\Large \Rightarrow x=1\Rightarrow \overrightarrow{IN}\left(6; \dfrac{27}{6}\right)$

$\Large \Rightarrow IN=\dfrac{15}{2}$

• $\Large MN_{\min}=IN-R=\dfrac{15}{2}-\dfrac{7}{2}=4$.