Cho hai mặt phẳng ( P ) và ( Q ) song song với nhau cắt khối cầu tâm O

MỤC LỤC
Câu hỏi:
Cho hai mặt phẳng (P) và (Q) song song với nhau cắt khối cầu tâm O bán kính R tạo thành hai hình tròn (C1)(C1) và (C2)(C2) cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn, đáy trùng với hình tròn còn lại. Biết diện tích xung quanh của hình nón là lớn nhất, khi đó thể tích khối trụ có hai đáy là hai hình tròn (C1)(C1) và (C2)(C2) bằng:
Đáp án án đúng là: A
Lời giải chi tiết:
Chọn A
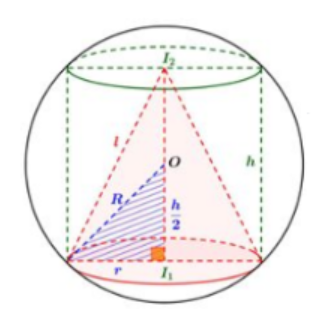
Gọi r, h, l lần lượt là bán kính đáy, chiếu cao và đường sinh của hình nón là I1,I2I1,I2, O lần lượt là tâm của hai đường tròn (C1),(C2)(C1),(C2) và mặt cầu.
Vì hai đường tròn (C1),(C2)(C1),(C2) có bán kính bằng nhau nên dễ dàng suy ra OI1=OI2=h2OI1=OI2=h2
Ta có r=√R2−h24⇒l=√h2+r2=√R2+3h24r=√R2−h24⇒l=√h2+r2=√R2+3h24
Diện tích xung quanh hình nón là:
Sxq=πrl=π.√R2−h24.√R2+3h24Sxq=πrl=π.√R2−h24.√R2+3h24
=π4√3.√(12R2−3h2).(4R2+3h2)≤2πR2√3=π4√3.√(12R2−3h2).(4R2+3h2)≤2πR2√3
SxqSxq lớn nhất bằng 2πR2√32πR2√3. Dấu “=” xảy ra khi và chỉ khi:
12R2−3h2=4R2+3h2⇔h=2R√3⇒r=R√6312R2−3h2=4R2+3h2⇔h=2R√3⇒r=R√63
Mà bán kính đáy và chiều cao của hình nón cũng chính là bán kính đáy và chiều cao hình trụ.
Vậy thể tích hình trụ V=π.r2.h=π.6R29.2R√3=4πR3√39V=π.r2.h=π.6R29.2R√3=4πR3√39
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , hình chiếu vuô
- Cho hình chóp S.ABC có SA=a√32SA=a√32 , các cạnh c
- Cho hai mặt cầu (S1)(S1) và (S2)(S2) đồng tâm I , có b
- Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng $
- Cho hình chóp S.ABC có đáy ABC là một tam giác đều cạnh bằng a . Cạnh