Cho đồ thị biểu diễn mối liên hệ giữa u và i trong mạch điện xoay chiề

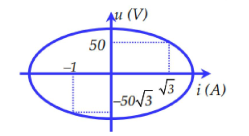
Cho đồ thị biểu diễn mối liên hệ giữa u và i trong mạch điện xoay chiều chỉ có L như hình vẽ. Xác định giá trị cảm kháng của cuộn cảm:

• A.

  A. $\Large 100\Omega.$

• B.

  B. $\Large 50\sqrt{2} \Omega.$

• C.

  C. $\Large 50\Omega.$

• D.

  D. $\Large 200\Omega.$

Đáp án C
Phương pháp giải: 
Đối với đoạn mạch chỉ chứa cuộn cảm: $\Large \left\{\begin{align} & u=U_0.cos(\omega t+\varphi) \\ & i=I_0.cos\bigg(\omega t+\varphi -\dfrac{\pi}{2}\bigg) \end{align}\right.$
Vì u và i vuông pha với nhau nên ta có $\Large \dfrac{u^2}{U_0^2}+\dfrac{i^2}{I_0^2}=1$ đồ thị u phụ thuộc vào I là một elip.
Từ đồ thị ta xác định được hai vị trí tọa độ: $\Large (u_1; i_1)=(50; \sqrt{3}); (u_2; i_2)=(-50\sqrt{3}; -1)$ thay vào phương trình trên tìm được $\Large U_0$ và $\Large I_0.$
Giải chi tiết: 
Đối với đoạn mạch chỉ chứa cuộn cảm: $\Large \left\{\begin{align} & u=U_0.cos(\omega t+\varphi) \\ & i=I_0.cos\bigg(\omega t+\varphi -\dfrac{\pi}{2}\bigg) \end{align}\right.$
Vì u và i vuông pha với nhau nên: $\Large \dfrac{u^2}{U_0^2}+\dfrac{i^2}{I_0^2}=1 \ (*)$
$\Large \rightarrow$ Đồ thị u phụ thuộc vào là một elip.
Từ đồ thị ta xác định được hai vị trí có tọa độ: $\Large \left\{\begin{align} & (u_1; i_1)=(50; \sqrt{3}) \\ & (u_2; i_2)=(-50\sqrt{3}; -1) \end{align}\right.$
Thay vào (*) được: $\Large \left\{\begin{align} & \dfrac{50^2}{U_0^2}+\dfrac{(\sqrt{3})^2}{I_0^2}=1 \\ & \dfrac{(50\sqrt{3})^2}{U_0^2}+\dfrac{(-1)^2}{I_0^2}=1 \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & U_0=100V \\ & I_0=2A \end{align}\right.$
Áp dụng định luật Ôm: $\Large I_0=\dfrac{U_0}{Z_L} \Rightarrow Z_L=\dfrac{U_0}{I_0}=\dfrac{100}{2}=50 \Omega$