Vị trí tương đối giữa 2 đường tròn
Lý thuyết về Vị trí tương đối giữa 2 đường tròn
1. Vị trí tương đối của hai đường tròn
Cho hai đường tròn $(O; R)$ và $(O’; R’)$ ta có :
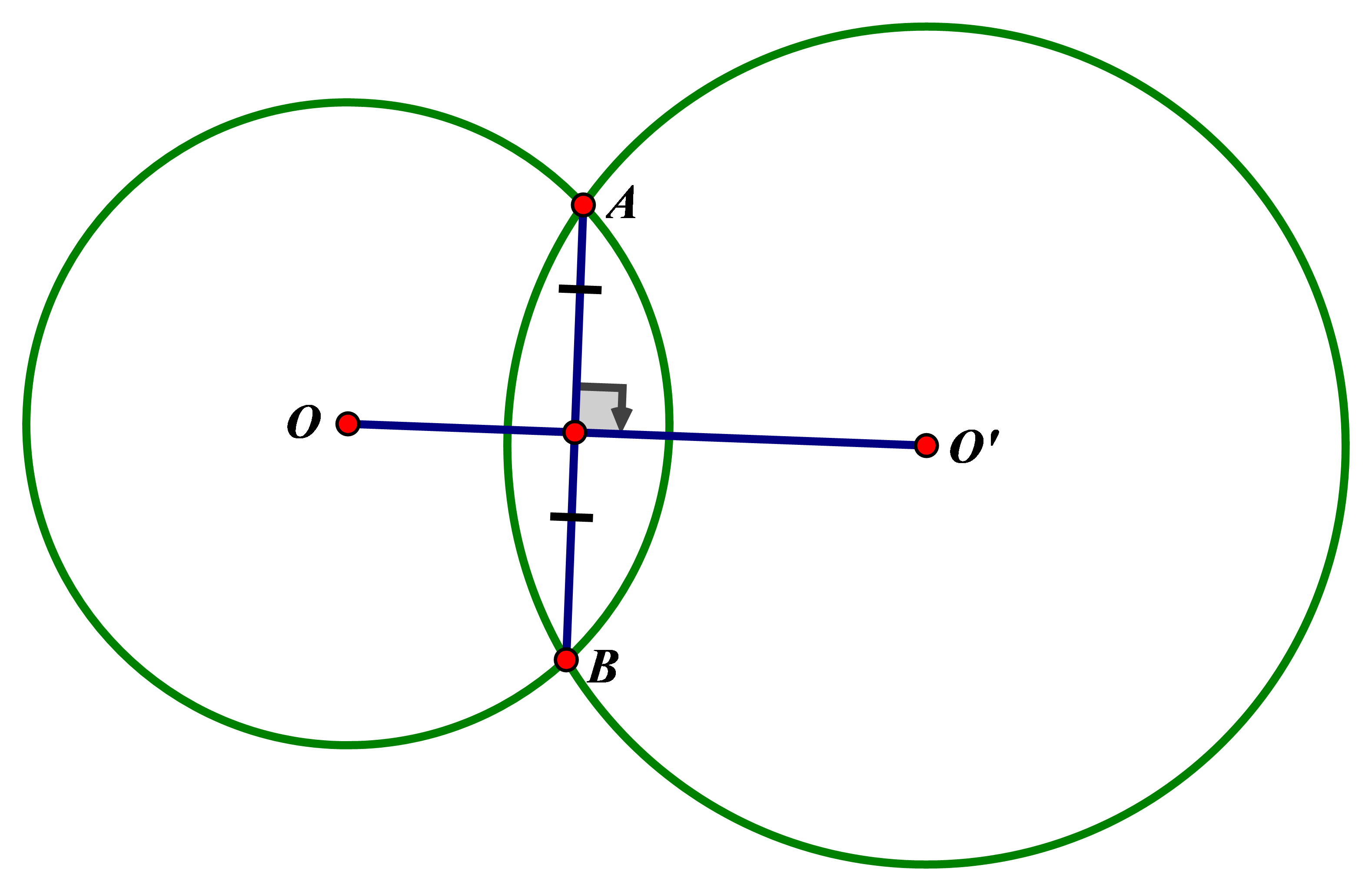
a) Nếu hai đường tròn cắt nhau thì: \[\left| {R - R'} \right| < OO' < R + R'\]
b) Nếu hai đường tròn tiếp xúc nhau thì :
– Hai đường tròn tiếp xúc trong: \[OO' = \left| {R - R} \right|\]
– Hai đường tròn tiếp xúc ngoài: \[OO' = R + R'\]
c) Nếu hai đường tròn không giao nhau thì:
– Hai đường tròn ngoài nhau: \[OO' > R + R'\]
– Hai đường tròn lồng nhau: \[OO' < \left| {R - R'} \right|\]
– Hai đường tròn đồng tâm: \[OO' = 0.\]
2. Định lí
– Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây cung.
– Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
Bài tập tự luyện có đáp án
Câu 1: Nếu hai đường tròn tiếp xúc nhau thì số điểm chung của hai đường tròn là
- A
- B
- C
- D
Hai đường tròn tiếp xúc nhau thì chúng có 1 điểm chung.
Câu 2: Cho hai đường tròn $ \left( O \right) $ và $ \left( O' \right) $ cắt nhau tại $ A,B $ . Tìm khẳng định sai:
- A
- B
- C
- D
Hai đường tròn $ \left( O \right) $ và $ \left( O' \right) $ cắt nhau tại $ A,B $ $ \Rightarrow $ đường thẳng $ OO' $ là trung trực $ AB $ hay $ A,B $ đối xứng nhau qua $ OO' $ .
Tam giác AOB cân ở O có $ OO'\bot AB $ nên $ OO' $ cũng là phân giác trong góc $ \widehat{AOB} $ .
Câu 3: Hai đường tròn $ \left( O \right) $ và $ \left( O' \right) $ tiếp xúc ngoài với nhau tại $ A $ . Đường thẳng d qua $ A $ ( $ d $ khác $ \text{OO }\!\!'\!\!\text{ } $ ) cắt $ \left( O \right) $ và $ \left( O' \right) $ lần lượt tại $ B,C $ . Khi đó:
- A
- B
- C
- D
$ \Delta OAB $ cân ở $ O $ nên $ \widehat{{{B}_{1}}}=\widehat{{{A}_{1}}} $
$ \Delta O'AC $ cân ở $ O' $ nên $ \widehat{{{C}_{1}}}=\widehat{{{A}_{2}}} $
Mà $ \widehat{{{A}_{1}}}=\widehat{{{A}_{2}}} $ (hai góc đối đỉnh).
Suy ra $ \widehat{{{B}_{1}}}=\widehat{{{C}_{1}}} $ mà hai góc này ở vị trí so le trong nên $ OB//O'C $
Câu 4: Chọn khẳng định sai:
- A
- B
- C
- D
Hai đường tròn cắt nhau thì có hai điểm chung. (đúng)
Hai đường tròn tiếp xúc nhau thì có 1 điểm chung. (đúng)
Hai đường tròn không giao nhau thì không có điểm chung. (đúng)
Hai đường tròn không tiếp xúc nhau thì cắt nhau. SAI vì chúng có thể không cắt nhau.
Câu 5: Hai đường tròn $ \left( O \right) $ và $ \left( O' \right) $ tiếp xúc nhau tại $ A. $ Khi đó
- A
- B
- C
- D
Hai đường tròn $ \left( O \right) $ và $ \left( O' \right) $ tiếp xúc nhau tại $ A $ thì $ A\in \text{OO}' $ .
Câu 6: Hai đường tròn $ \left( O;6 \right) $ và $ \left( O';4 \right) $ tiếp xúc ngoài với nhau tại $ A $ . Đường thẳng d qua $ A $ ( $ d $ khác $ \text{OO }\!\!'\!\!\text{ } $ ) cắt $ \left( O \right) $ và $ \left( O' \right) $ lần lượt tại $ B,C $ .Biết $ AB=8 $ . Tính $ AC $
- A
- B
- C
- D
Ta có hình vẽ như sau
$ \Delta OAB $ cân ở $ O $ nên $ \widehat{{{B}_{1}}}=\widehat{{{A}_{1}}} $
$ \Delta O'AC $ cân ở $ O' $ nên $ \widehat{{{C}_{1}}}=\widehat{{{A}_{2}}} $
Mà $ \widehat{{{A}_{1}}}=\widehat{{{A}_{2}}} $ (hai góc đối đỉnh).
Suy ra $ \widehat{{{B}_{1}}}=\widehat{{{C}_{1}}} $ suy ra $ \Delta AOB\sim \Delta AO'C\left( g.g \right) $
$ \Rightarrow \dfrac{{AO}}{{AB}} = \dfrac{{AO'}}{{AC}} \Rightarrow AC = \dfrac{{AB.AO'}}{{AO}} = \dfrac{{8.4}}{6} = \dfrac{{16}}{3}$