Thể tích của hình chóp đều
Lưu về Facebook:
Lý thuyết về Thể tích của hình chóp đều
Thể tích của hình chóp đều là: $V=\dfrac{1}{3}S.h$ ( $S$ là diện tích đáy, $h$ là chiều cao).
Bài tập tự luyện có đáp án
Câu 1: Cho hình chóp đều $S.ABC$ có cạnh đáy bằng $a$, chiều cao $SH = a$. Hỏi thể tích của khối chóp bằng bao nhiêu?
- A
- B
- C
- D
Do đáy là tam giác đều cạnh bằng $a$ nên diện tích đáy $S = \dfrac{a^2\sqrt{3}}{4}$.
Khi đó thể tích $V = \dfrac{1}{3} Sh = \dfrac{a^3\sqrt{3}}{12}$.
Câu 2: Cho hình lăng trụ đứng $ABC.A'B'C'$ có thể tích $V$. Hình chóp $S.ABC$ có đỉnh $S$ là tâm của tam giác $A'B'C'$ có thể tích bằng bao nhiêu?
- A
- B
- C
- D
Câu 3: Thể tích của hình chóp tứ giác đều có chiều cao bằng $6cm$, cạnh đáy bằng $4cm$ bằng bao nhiêu?
- A
- B
- C
- D
Diện tích đáy là $S = 4^2 = 16cm^2$.
Thể tích là: $V = \dfrac{1}{3} Sh = 32cm^3$.
Câu 4: Phát biểu nào sau đây đúng:
- A
- B
- C
- D
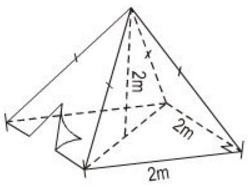
Câu 5: 
Một cái lều có các kích thước như hình vẽ. Hỏi thể tích phần không khí phía bên tronng lều bằng bao nhiêu?
Một cái lều có các kích thước như hình vẽ. Hỏi thể tích phần không khí phía bên tronng lều bằng bao nhiêu?- A
- B
- C
- D
Diện tích đáy bằng $4m^2$ do đáy là hình vuông cạnh bằng $2m$.
Khi đó thể tích được tính theo công thức $V = \dfrac{1}{3} Sh = \dfrac{8}{3} m^3$.
Câu 6: Cho chóp $S.ABCD$ có cạnh đáy $AB = a$, thể tích $V = a^3$. Độ dài cạnh bên $SA$ bằng
- A
- B
- C
- D
Gọi $O$ là tâm của tứ giác $ABCD$. Ta có chiều cao của hình chóp là: $SO = \dfrac{3V}{AB^2} = 3a$.
Khi đó cạnh bên $SA = \sqrt{SO^2 + OA^2} = \dfrac{a\sqrt{38}}{2}$.
Câu 7: Hình chóp đều có diện tích đáy là S, chiều cao h. Thể tích hình chóp đều đó là:
- A
- B
- C
- D