Bất phương trình bậc nhất một ẩn
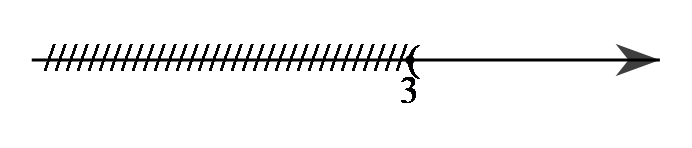
Lý thuyết về Bất phương trình bậc nhất một ẩn
Định nghĩa bất phương trình bậc nhất một ẩn: Bất phương trình dạng ax+b<0 (hoặc ax+b>0, ax+b≤0, ax+b≥0) trong đó a và b là hai số đã cho, a≠0, được gọi là bất phương trình bậc nhất một ẩn.
Hai quy tắc biến đổi bất phương trình:
- Quy tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
- Quy tắc nhân với một số: Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
- Giữ nguyên chiều bất phương trình nếu số đó dương.
- Đổi chiều bất phương trình nếu số đó âm.
Bài tập tự luyện có đáp án
Câu 1: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn? Hãy chọn câu đúng?
- A
- B
- C
- D
Bất phương trình dạng ax+b>0 (hoặc ax+b<0,ax+b≥0,ax+b≤0 ) trong đó a và b là hai số đã cho, a≠0 , gọi là bất phương trình bậc nhất một ẩn.
Nên y<10−2y là bất phương trình bậc nhất một ẩn.
Câu 2: Hãy chọn câu đúng, x=−3 là một nghiệm của bất phương trình
- A
- B
- C
- D
+ Thay x=−3 vào bất phương trình 2x+1>5 ta được 2.(−3)+1>5⇔−5>5 (vô lý) nên x=−3 không là nghiệm của bất phương trình 2x+1>5 .
+ Thay x=−3 vào bất phương trình 7−2x<10−x ta được 7−2.(−3)<10−(−3)⇔13<13 (vô lý) nên x=−3 không là nghiệm của bất phương trình 7−2x<10−x .
+ Thay x=−3 vào bất phương trình 2+x<2+2x ta được 2+(−3)<2+2.(−3)⇔−1<−4 (vô lý) nên x=−3 không là nghiệm của bất phương trình 2+x<2+2x .
+ Thay x=−3 vào bất phương trình −3x>4x+3 ta được −3.(−3)>4.(−3)+3⇔9>−9 (luôn đúng) nên x=−3 là nghiệm của bất phương trình −3x>4x+3 .
Câu 3: Biểu diễn tập nghiệm của bất phương trình x≥8 trên trục số, ta được
- A
- B
- C
- D
Ta biểu diễn x≥8 trên trục số như sau
Câu 4: Có bao nhiêu giá trị nguyên của x thỏa mãn cả hai bất phương trình sau: x+25−3x−74>−5 và 3x5−x−43+x+26>6
x+25−3x−74>−5 và 3x5−x−43+x+26>6
- A
- B
- C
- D
Ta có
x+25−3x−74>−54x+820−15x−3520>−10020⇔−11x+43+10020>0⇔−11x+143>0⇔x<13
Lại có
3x5−x−43+x+26>6⇔18x30−10x−4030+5x+1030>18030⇔13x−13030>0⇔13x−130>0⇔x>10
Vậy tập hợp các giá trị của x thỏa mãn cả hai bất phương trình là:
S={11;12}
Câu 5: Bất phương trình nào sau đây có cả nghiệm âm và nghiệm dương?
- A
- B
- C
- D
- 32x<−9⇔x<−6. Bất phương trình chỉ có nghiệm âm.
- 2x+45>95⇔x>1. Bất phương trình chỉ có nghiệm dương.
- 6−35x<4⇔x>103. Bất phương trình chỉ có nghiệm dương.
- 5+23x>3⇔x>−3. Bất phương trình có cả nghiệm âm và dương.
Câu 6: Bất phương trình x−2>4 , phép biến đổi nào sau đây là đúng?
- A
- B
- C
- D
Ta có x−2>4 , chuyển −2 từ trái sang vế phải ta được x>4+2 .
Câu 7: Trong các bất phương trình sau, đâu là bất phương trình bậc nhất một ẩn
- A
- B
- C
- D
Bất phương trình dạng ax+b<0 (hoặc ax+b>0, ax+b≤0, ax+b≥0) trong đó a và b là hai số đã cho, a≠0, được gọi là bất phương trình bậc nhất một ẩn.
Câu 8: Hãy chọn câu đúng. Tập nghiệm của bất phương trình 1−3x≥2−x là
- A
- B
- C
- D
1−3x≥2−x
⇔1−3x+x−2≥0
⇔−2x−1≥0
⇔−2x≥1
⇔x≤−12 .
Vậy tập nghiệm của bất phương trình S={x∈R|x≤−12} .
Câu 9: Tìm x biết: 8−4x<0 .
- A
- B
- C
- D
Ta có
8−4x<0⇔8<4x⇔2<x
Câu 10: Điều kiện của x để P=x−3x+1 có giá trị lớn hơn 1 là
- A
- B
- C
- D
Ta có P>1⇔x−3x+1>1⇔x−3x+1−1>0⇔x−3−x−1x+1>0⇔−4x+1>0 .
Vì −4<0 nên ⇒x+1<0⇔x<−1 .
Câu 11: Bất phương trình nào sau đây chỉ có nghiệm dương?
- A
- B
- C
- D
- x−2>3x+6⇔2x<−8⇔x<−4. Bất phương trình chỉ có nghiệm âm.
- 5x>2x+6⇔3x>6⇔x>2. Bất phương trình chỉ có nghiệm dương.
- x+1<4−3x⇔4x<3⇔x<34. Bất phương trình có cả nghiệm âm và nghiệm dương.
- x+1≥0⇔x>−1. Bất phương trình có cả nghiệm âm và nghiệm dương.
Câu 12: Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
- A
- B
- C
- D
Bất phương trình bậc nhất một ẩn là bất phương trình có dạng ax+b>0 hoặc ax+b<0,ax+b≥0,ax+b≤0 trong đó a≠0.
Câu 13: Để bất phương trình (m−1)x+2>0 là bất phương trình bậc nhất thì điều kiện của m là:
- A
- B
- C
- D
Để bất phương trình (m−1)x+2>0 là bất phương trình bậc nhất thì m≠1 .
Câu 14: Bất phương trình x−2<1 tương đương với bất phương trình
- A
- B
- C
- D
Ta có x−2<1⇔x−2+1<1+1⇔x−1<2 .
Chuyển vế −2 từ vế trái sang vế phải thì phải đối dấu ta được
Bpt ⇔x<1+2⇔x<3 .
Câu 15: Chọn câu đúng. Bất phương trình bậc nhất 2x−2>4 có tập nghiệm biểu diễn bởi hình vẽ
Bất phương trình bậc nhất 2x−2>4 có tập nghiệm biểu diễn bởi hình vẽ
- A
- B
- C
- D
Giải bất phương trình ta được: 2x−2>4⇔2x>6⇔x>3 .
Biểu diễn trên trục số

Câu 16: Trong các phương trình sau, đâu không phải là bất phương trình bậc nhất một ẩn:
- A
- B
- C
- D
Câu 17: Hình biểu diễn tập nghiệm của bất phương trình 3x+6≥−x+14 là
- A
- B
- C
- D
Bất phương trình đã cho có thể viết lại thành 4x≥8⇔x≥2.
Câu 18: Hình biểu diễn tập nghiệm của bất phương trình 3x−1>2 là:
- A
- B
- C
- D
Bất phương trình đã cho tương đương với x>1.
Câu 19: Hình biểu diễn tập nghiệm của bất phương trình 3x+1≤x+3 là
- A
- B
- C
- D
Bất phương trình đã cho tương đương với x≤1.