Tọa độ của điểm
Lý thuyết về Tọa độ của điểm
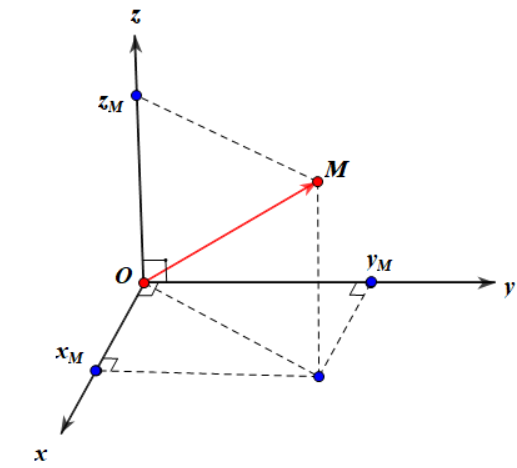
Trong không gian tọa độ $Oxyz$, mỗi điểm $M$ được hoàn toàn xác định bởi vecto $\overrightarrow{OM}$. Bởi vậy, nếu $(x,y,z)$ là tọa độ của $\overrightarrow{OM}$ thì ta cũng nói $(x,y,z)$ là tọa độ của điểm $M$ và ký hiệu là $M=(x,y,z)$ hoặc $M(x,y,z)$.
Như vậy: $M=\left( x;y;z \right)\Leftrightarrow \overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{i}+z\overrightarrow{k}$.
Số $x$ gọi là hoành độ, $y$ là tung độ và $z$ là cao độ của điểm $M$
Chú ý. Cho điểm $M(a; b; c)$
- Hình chiếu của điểm $M$ lên các trục tọa độ $Ox, Oy, Oz$ lần lượt là $M_1(a;0;0)$, $M_2(0;b;0)$, $M_3(0;0;c)$.
- Khoảng cách từ $M$ đến các trục tọa độ $Ox, Oy, Oz$ lần lượt là $d_1 = \sqrt{b^2 + c^2}$, $d_2 = \sqrt{c^2 + a^2}$, $d_3 = \sqrt{a^2 + b^2}$.
- Hình chiếu của điểm $M$ lên các mặt phẳng tọa độ $(Oxy); (Oyz); (Ozx)$ lần lượt là $M_1'(a;b;0)$, $M_2'(0;b;c)$, $M_3'(a;0;c)$.
- Khoảng cách từ $M$ đến các mặt phẳng tọa độ $(Oxy); (Oyz); (Ozx)$ lần lượt là $h_1 =|c|$, $h_2 = |a|$, $h_3 = |b|$.
Bài tập tự luyện có đáp án
Câu 1: Hình chiếu của điểm $M\left( 3;2;-1 \right)$ lên trục \( {Oz}\) có tọa độ là
- A
- B
- C
- D
Ta có tọa độ hình chiếu của điểm $M\left( x;y;z \right)$ lên trục \( {Oz}\) có dạng: $\left( 0;0;z \right)$
$\Rightarrow \left( 0;0;-1 \right)$ là đáp án
Câu 2: Cho 2 điểm \(M\left( -2;3;1 \right),N\left( 5;6;-2 \right)\) có hình chiếu vuông góc lên trục $Ox$ lần lượt là $A,B$ khi đó tỷ số: $\dfrac{OA}{OB}=?$
- A
- B
- C
- D
Tọa độ $\left\{ \begin{align}
& A\left( -2;0;0 \right) \\
& B\left( 5;0;0 \right) \\
\end{align} \right.\Rightarrow \dfrac{OA}{OB}=\dfrac{2}{5}$
Câu 3: Trong không gian \(Oxyz\), cho điểm $M\left( 2015;2016;2017 \right)$ , tọa độ hình chiếu của M lên trục Oz là:
- A
- B
- C
- D
Khi chiếu điểm $M$ xuống trục Oz thì hoành độ và tung độ của điểm đó bằng 0, cao độ bằng 2017, vậy tọa độ hình chiếu của $M$ trên Oz là $\left( 0;0;2017 \right)$
Câu 4: Tọa độ hình chiếu của \(A\left( 1;2;-3 \right)\) lên mặt Oxy là:
- A
- B
- C
- D
Khi chiếu một điểm lên mặt Oxy thì cao độ z của điểm đó bị triệt tiêu. Áp dụng trực tiếp cho bài này ta có hình chiếu của \(A\left( 1;2;-3 \right)\) có tọa độ là \(\left( 1;2;0 \right)\)
Câu 5: Hình chiếu của điểm $M\left( 0;3;-4 \right)$ lên trục \(Oy\) có tọa độ là
- A
- B
- C
- D
Ta có tọa độ hình chiếu của điểm $M\left( x;y;z \right)$ lên trục \(Oy\) có dạng: $\left( 0;y;0 \right)$
$\Rightarrow \left( 0;3;0 \right)$ là đáp án
Câu 6: Hình chiếu của điểm $A\left( 5;6;-7 \right)$ lên trục \( Ox\) có tọa độ là
- A
- B
- C
- D
Ta có tọa độ hình chiếu của điểm $A\left( x;y;z \right)$ lên trục \( Ox\) có dạng: $\left( x;0;0 \right)$
$\Rightarrow \left( 5;0;0 \right)$ là đáp án