Sự tương giao của các đồ thị
Lý thuyết về Sự tương giao của các đồ thị
Sự tương giao của các đồ thị
Giả sử hàm số y=f(x)y=f(x) có đồ thị là (C1)(C1) và hàm số y=g(x)y=g(x) có đồ thị là (C2)(C2)
Hoành độ giao điểm của (C1)(C1) và (C2)(C2) là nghiệm của phương trình f(x)=g(x)f(x)=g(x)
Giả sử phương trình trên có các nghiệm là x0,x1,....x0,x1,....
Khi đó , các giao điểm của (C1)(C1) và (C2)(C2) là M0(x0;f(x0)),M1(x1;f(x)),....M0(x0;f(x0)),M1(x1;f(x)),....
Số giao điểm chính là số nghiệm của phương trình hoành độ giao điểm
Ví dụ: Chứng minh rằng đồ thị (C)(C) của hàm số y=x−1x+1y=x−1x+1 luôn luôn cắt đường thẳng (d):y=m(d):y=m với mọi giá trị của mm
Giải
(C)(C)luôn cắt (d)(d) nếu phương trình: x−1x+1=m−xx−1x+1=m−x (1) có nghiệm với mọi mm
Ta có x−1x+1=m−x⇔{x−1=(x+1)(m−x)x≠−1⇔{x2+(2−m)x−m−1=0(2)x≠−1
Xét phương trình (2) , ta có Δ=m2+8>0với mọi giá trị của m và x=−1 không thỏa mãn (2) nên phương trình luôn có hai nghiệm khác -1 . Vậy (C) và (d) luôn cắt nhau tại hai điểm
Bài tập tự luyện có đáp án
Câu 1: Cho hàm số y=2+x3−2x và đường thẳng y=1 . Số giao điểm của hai đồ thị là:
- A
- B
- C
- D
Phương trình hoành độ giao điểm:
2+x3−2x=1⇔{x≠323−2x=x+2⇔x=13
Hai đồ thị giao nhau tại 1 điểm.
Câu 2: Số giao điểm của đồ thị hàm số y=(x2−1)2 và trục hoành là
- A
- B
- C
- D
Câu 3: Cho hàm số y=1−2xx+2 và đường thẳng y=x−1 . Tổng hoành độ giao điểm của hai đồ thị là:
- A
- B
- C
- D
Phương trình hoành độ giao điểm:
1−2xx+2=x−1⇔{x≠−2x2+x−2=1−2x⇔[x1=−3+√212x2=−3−√212⇔x1+x2=−3
Câu 4: Số giao điểm của đồ thị hàm số y=x3−x và trục Ox là
- A
- B
- C
- D
Câu 5: Đồ thị hàm số y=x4+2x2−3 cắt trục tung tại điểm M khi đó tung độ điểm M bằng
- A
- B
- C
- D
Do giao cắt với trục tung nên x=0 nên thay trực tiếp vào ta được y=04+2.02−3=−3.
Câu 6: Cho hàm số y=(x−2)(x2+1) có đồ thị (C). Mệnh đề nào dưới đây đúng ?
Cho hàm số y=(x−2)(x2+1) có đồ thị (C). Mệnh đề nào dưới đây đúng ?
- A
- B
- C
- D
Phương trình hoành độ giao điểm của (C) Với trục hoành là (x−2)(x2+1)=0⇔x=2Vậy (C) cắt trục hoành tại một điểm
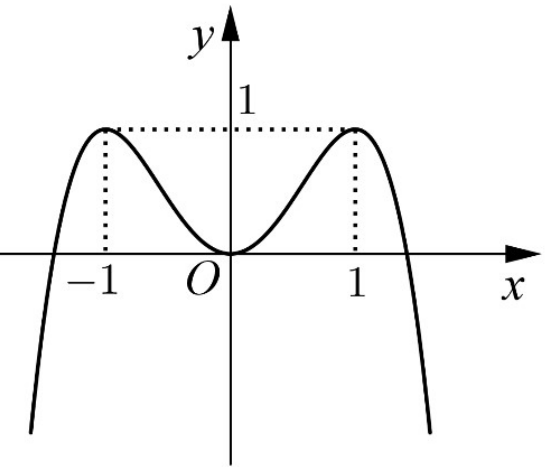
Câu 7:  Cho hàm số y=−x4+2x2 có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình −x4+2x2=m có bốn nghiệm thực phân biệt.
Cho hàm số y=−x4+2x2 có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình −x4+2x2=m có bốn nghiệm thực phân biệt.
 Cho hàm số y=−x4+2x2 có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình −x4+2x2=m có bốn nghiệm thực phân biệt.
Cho hàm số y=−x4+2x2 có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình −x4+2x2=m có bốn nghiệm thực phân biệt.- A
- B
- C
- D
Nhìn trên đồ thị ta thấy phương trình có bốn nghiệm thực phân biệt khi 0<m<1.
Câu 8: Số giao điểm nhiều nhất của đồ thị hàm số y=ax+bcx+d(c≠0,ad−bc≠0) với hai trục tọa độ là:
- A
- B
- C
- D
Đồ thị hàm bậc nhất trên bậc nhất cắt hai trục tọa độ nhiều nhất tại hai điểm.
Câu 9: Cho hàm số y=x−21−x và đường thẳng y=2x−3 . Tổng khoảng cách từ các giao điểm của hai đồ thị đến các trục tọa độ bằng
- A
- B
- C
- D
Phương trình hoành độ giao điểm:
x−21−x=2x−3⇔{x≠1−2x2+5x−3=x−2⇔[x=2+√22⇒y=√2−1x=2−√22⇒y=−√2−1
⇒ Tổng khoảng cách từ các giao điểm đến các trục tọa độ bằng
|x1|+|x2|+|y1|+|y2|=2√2+2
Câu 10:  Cho hàm số y=f(x) có bảng biến thiên như hình vẽ.
Có bao nhiêu giá trị nguyên của m để đường thẳng y=m cắt đồ thị hàm số tại ba điểm phân biệt?
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ.
Có bao nhiêu giá trị nguyên của m để đường thẳng y=m cắt đồ thị hàm số tại ba điểm phân biệt?
 Cho hàm số y=f(x) có bảng biến thiên như hình vẽ.
Có bao nhiêu giá trị nguyên của m để đường thẳng y=m cắt đồ thị hàm số tại ba điểm phân biệt?
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ.
Có bao nhiêu giá trị nguyên của m để đường thẳng y=m cắt đồ thị hàm số tại ba điểm phân biệt?- A
- B
- C
- D
Từ BBT ta thấy ycbt ⇔0<m<3Vậy có 2 giá trị nguyên của m