Khái niệm hai tam giác đồng dạng
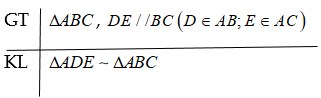
Lý thuyết về Khái niệm hai tam giác đồng dạng
1. Định nghĩa hai tam giác đồng dạng
Hai tam giác được gọi là đồng dạng với nhau nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Tam giác $A'B'C'$ gọi là đồng dạng với tam giác $ABC$ nếu:
\[\widehat {A'} = \widehat A;\widehat {B'} = \widehat B;\widehat {C'} = \widehat C;\dfrac{{A'B'}}{{AB}} = \dfrac{{B'C'}}{{BC}} = \dfrac{{C'A'}}{{CA}}\]
Kí hiệu tam giác đồng dạng: $\Delta A{\rm{'}}B{\rm{'}}C' \sim \Delta ABC$
Tỉ số: $\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{C'A'}{CA}=k$ gọi là tỉ số đồng dạng.
2. Tính chất hai tam giác đồng dạng
Hai tam giác $A’B’C’$ và $ABC$ đồng dạng có một số tính chất:
1) $\Delta A{\rm{'}}B{\rm{'}}C' \sim \Delta ABC$
2) Nếu \[\Delta A'{\rm{B'C'}} \sim \Delta {\rm{ABC}} \Rightarrow \Delta {\rm{ABC}} \sim \Delta {\rm{A'B'C'}}\]
3) Nếu \[\Delta A'B'C' \sim \Delta A{\rm{''B''C'';}}\Delta {\rm{A''B''C''}} \sim \Delta {\rm{ABC}} \Rightarrow \Delta {\rm{A'B'C'}} \sim \Delta {\rm{ABC}}\]
3 . Định lí hai tam giác đồng dạng
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
Bài tập tự luyện có đáp án
Câu 1: Hai tam giác $ ABC $ và $ A'B'C' $ có $ \widehat{BAC}=\widehat{B'A'C'}={{90}^{0}} $ . $ AB=4cm $ , $ BC=5cm $ , $ A'B'=8cm,A'C'=6cm $ . Khẳng định nào sau đây đúng?
- A
- B
- C
- D
Ta có:
$ AC=\sqrt{B{{C}^{2}}-A{{B}^{2}}}=\sqrt{{{5}^{2}}-{{4}^{2}}}=3 $
$ B'C{{'}^{2}}=\sqrt{A'B{{'}^{2}}+A'C{{'}^{2}}}=\sqrt{{{8}^{2}}+{{6}^{2}}}=10 $
Ta có: $ \dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}=\dfrac{1}{2} $ $ \Rightarrow \Delta ABC\sim \Delta A'B'C'\left( c.c.c \right) $
Câu 2: Cho tam giác $ ABC $ . $ M,N,P $ lần lượt là trung điểm $ AB,BC,CA $ . Khẳng định nào sau đây đúng?
- A
- B
- C
- D
Chú ý rằng, gọi tên 2 tam giác đồng dạng thì ta phải để các đỉnh tương ứng.
$ \Delta APM\sim \Delta ABC $ theo tỉ số đồng dạng là $ \dfrac{1}{2} $ là sai vì $ \Delta AMP\sim \Delta ABC $ mới đúng.
Tương tự $ \Delta MNB\sim \Delta ABC $ là sai (đúng phải là $ \Delta MBN\sim \Delta ABC $ ).
$ \Delta NPC\sim \Delta ABC $ là sai (đúng phải là $ \Delta PNC\sim \Delta ABC $ ).
$ \Delta NPM\sim \Delta ABC $ theo tỉ số đồng dạng là $ \dfrac{1}{2} $ là đúng.
Câu 3: Cho hai tam giác $ ABC $ và $ MNP $ . Biết $ AB=4,BC=5,CA=6 $ và $ MP=8,NP=12,MN=10 $ . Khẳng định nào sau đây đúng?
- A
- B
- C
- D
Xét tam giác $ ABC $ và $ PMN $ có
$ \dfrac{AB}{PM}=\dfrac{BC}{MN}=\dfrac{CA}{NP}=\dfrac{1}{2} $
$ \Rightarrow \Delta ABC\sim \Delta PMN\left( c.c.c \right) $
Xem thêm các bài tiếp theo bên dưới