Diện tích hình chữ nhật
Lý thuyết về Diện tích hình chữ nhật
Công thức tính diện tích hình chữ nhật
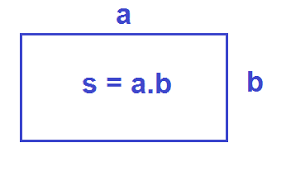
Diện tích hình chữ nhật bằng tích hai kích thước của nó: S=a.bS=a.b
(SS là diện tích, aa là chiều dài, bb là chiều rộng)
Bài tập tự luyện có đáp án
Câu 1: Diện tích hình chữ nhật giảm bao nhiêu phần trăm nếu mỗi cạnh giảm 10%
- A
- B
- C
- D
Gọi độ dài cạnh hình chữ nhật là a và b. Nếu mỗi cạnh giảm 10%10% thì độ dài mỗi cạnh sau khi giảm là: a−a.10%;b−b.10%a−a.10%;b−b.10%
Phần diện tích giảm là:
ab−(a−a.10%)(b−b.10%)=ab−90%a.90%b=ab−90100.90100ab=19100ab
Vậy diện tích tăng thêm 19% so với diện tích ban đầu.
Câu 2: Diện tích hình chữ nhật thay đổi như thế nào nếu chiều dài tăng 2 lẩn, chiều rộng không thay đổi
- A
- B
- C
- D
Gọi HCN ban đầu có diện tích S, chiều dài a, chiều rộng b
Khi đó chiều dài, rộng và diện tích HCN sau khi thay đổi là
a′=2a,b′=b⇒S′=a′.b′=2ab=2S .
Vậy diện tích hình mới bằng 2 lần diện tích hình đã cho
Câu 3: Diện tích hình chữ nhật thay đổi như thế nào nếu chiều dài không đổi, chiều rộng giảm đi 3 lần.
Chọn khẳng định đúng.
- A
- B
- C
- D
Gọi HCN ban đầu có diện tích S, chiều dài a, chiều rộng b
Khi đó chiều dài, rộng và diện tích HCN sau khi thay đổi là
a′=a,b′=b3⇒S′=a′.b′=13ab=13S .
Vậy diện tích HCN mới giảm 3 lần so với diện tích HCN ban đầu.
Câu 4:
Diện tích hình chữ nhật thay đổi như thế nào nếu chiều dài tăng 2 lần, chiều rộng giảm đi 4 lần
- A
- B
- C
- D
Gọi HCN ban đầu có diện tích S, chiều dài a, chiều rộng b
Khi đó chiều dài, rộng và diện tích HCN sau khi thay đổi là
a′=2a,b′=b4⇒S′=a′.b′=12ab=12S .
Vậy diện tích hình mới bằng 12 lần diện tích hình đã cho
Câu 5: Diện tích hình chữ nhật tăng bao nhiêu phần trăm nếu mỗi cạnh tăng 20%?
- A
- B
- C
- D
Gọi độ dài cạnh hình chữ nhật là a và b. Nếu mỗi cạnh tăng 20% thì độ dài mỗi cạnh sau khi tăng1à: a+a.20%;b+b.20%
Phần diện tích tăng thêm là:
(a+a.20%)(b+b.20%)−ab=120%a.120%b−ab=120100.120100ab−ab=44100ab
Vậy diện tích tăng thêm 44% so với diện tích ban đầu.
Câu 6: Nền của một phòng khách có dạng hình chữ nhật, với chiều rộng đo được là 6m và chiều dài là 8m. Để có thể lát kín nền đó cần bao nhiêu viên gạch có hình vuông, với cạnh là 50cm
- A
- B
- C
- D
Ta có diện tích nền phòng khách là: 6.8=48m2
Số viên gạch cần dùng là 480.52=192 viên
Câu 7: Có thể dùng kéo cắt ít nhất bao nhiêu lần và chỉ cắt theo đường thẳng để chia một hình chữ nhật thành hai mảnh để ghép lại được một tam giác
- A
- B
- C
- D
Ta có thể cắt 1 lần theo hình ảnh dưới

Câu 8: Gọi a,b là các cạnh của một hình chữ nhật, biết tỉ số các cạnh là 4/5 và diện tích của nó là 80cm2 . Khi nó a+b bằng
- A
- B
- C
- D
Ta có {ab=45ab=80⇔{a=4b54b5.b=80⇔{a=4b5b2=100⇔{a=8b=10
Câu 9: Có thể dùng kéo cắt ít nhất bao nhiêu lần và chỉ cắt theo đường thằng, chai một hình chữ nhật thành ba mảnh để ghép lại được một tam giác thường
- A
- B
- C
- D
Ta có thể dùng 2 nét cắt như hình

Câu 10: Cho hình vuông ABCD, biết độ dài đường chéo là h. Khi đó diện tích ABCD là
- A
- B
- C
- D
Sử dụng định lý pitago cho tam giác ABC, AC=h ta có
AB2+BC2=AC2⇒2AB2=h2⇒AB=h√2⇒SABCD=(h√2)2=h22
Câu 11: Cho hình chữ nhật ABCD . Trên cạnh AB lấy hai điểm M, N sao cho AM=MN=NB . Gọi P là điểm chia cạnh DC thành 2 phần bằng nhau. ND cắt MP tại O, nối PN (hình vẽ). Biết diện tích tam giác DOP lớn hơn diện tích tam giác MON là 3,5cm2 . Diện tích hình chữ nhật ABCD là


- A
- B
- C
- D
Hai tam giác MPN và NPD có phần chung là tam giác NOP.
Mà SDOP−SMON=3,5cm2 . Nên SNPD−SMPN=3,5cm2 .
Mặt khác SNPD=12BC.DP=12BC.12DC=14SABCD
SMPN=12BC.MN=12BC.13AB=16SABCD
Từ đó 14SABCD−16SABCD=112SABCD=3,5cm2
⇒SABCD=3,5.12=42(cm2)
Xem thêm các bài tiếp theo bên dưới