Diện tích đa giác
Lý thuyết về Diện tích đa giác
Tính chất
– Hai tam giác bằng nhau thì có diện tích bằng nhau.
– Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích của những đa giác đó.
Cách tính diện tích đa giác
Việc tính diện tích đa giác thường được quy về tính diện tích tam giác (tam giác vuông), hoặc diện tích các hình đã biết công thức cách tính (hình chữ nhật, hình thang, hình thoi....)
Bài tập tự luyện có đáp án
Câu 1: Cho hình chữ nhật $ ABCD $ . Trên cạnh $ AB $ lấy $ M $ . Tìm vị trí của $ M $ để $ {{S}_{MBC}}=\dfrac{1}{4}{{S}_{ABCD}} $ .
- A
- B
- C
- D

Ta có $ {{S}_{ABCD}}=AB.BC;{{S}_{MBC}}=\dfrac{1}{2}MB.BC $
Để $ {{S}_{MBC}}=\dfrac{1}{4}{{S}_{ABCD}}\Leftrightarrow \dfrac{1}{2}MB.BC=\dfrac{1}{4}AB.BC\Leftrightarrow MB=\dfrac{1}{2}AB $
Mà $ M\in AB $ nên $ M $ là trung điểm đoạn $ AB $ .
Câu 2: Cho hình chữ nhật $ ABCD $ có $ AD=8cm,AB=9cm $ . Các điểm $ M,N $ trên đường chéo $ BD $ sao cho $ BM=MN=ND $ . Tính diện tích tam giác $ CMN $ .



- A
- B
- C
- D
+ Ta có $ AB=CD=9cm;BC=AD=8cm $ nên
$ {{S}_{BCD}}=\dfrac{1}{2}BC.DC=\dfrac{1}{2}.8.9=36c{{m}^{2}} $ .
+ Kẻ $ CH\bot BD $ tại $ H $
+ Ta có $ {{S}_{BCD}}=\dfrac{1}{2}CH.BD;{{S}_{CMN}}=\dfrac{1}{2}CH.MN $ mà $ MN=\dfrac{1}{3}BD\Rightarrow {{S}_{CMN}}=\dfrac{1}{2}{{S}_{BCD}}=\dfrac{1}{3}.36=12c{{m}^{2}} $ .
Câu 3: Một tam giác có độ dài ba cạnh là $ 12cm,5cm,13cm $ . Diện tích tam giác đó là
- A
- B
- C
- D
Ta có: $ {{5}^{2}}+{{12}^{2}}=169;{{13}^{2}}=169\Rightarrow {{5}^{2}}+{{12}^{2}}={{13}^{2}} $
Do đó đây tam giác đã cho là tam giác vuông có hai cạnh góc vuông là $ 5cm $ và $ 12cm $ .
Diện tích tam giác đó là: $ \dfrac{1}{2}.12.5=30(c{{m}^{2}}) $ .
Câu 4: Cho hình bình hành ABCD có diện tích S và M, N tương ứng là trung điểm của các cạnh AD, CD. Khi đó, diện tích của tứ giác BMDN theo S bằng
- A
- B
- C
- D

Gọi $ {{h}_{1}};{{h}_{2}} $ lần lượt là khoảng cách từ B xuống AD, Chọn D, khi đó ta có:
$ \begin{array}{l} {{S}_{ABM}}=\dfrac{1}{2}{{h}_{1}}.AM=\dfrac{1}{4}{{h}_{1}}.AD=\dfrac{1}{4}S \\ {{S}_{BNC}}=\dfrac{1}{2}{{h}_{2}}.NC=\dfrac{1}{4}{{h}_{2}}.NC=\dfrac{1}{4}S \\ \Rightarrow {{S}_{BMDN}}={{S}_{ABCD}}-{{S}_{ABM}}-{{S}_{BNC}}=S-\dfrac{1}{4}S-\dfrac{1}{4}S=\dfrac{1}{2}S \end{array} $
Câu 5: Cho đa giác $ ABCD $ như hình vẽ. Diện tích $ ABCD $ bằng theo đơn vị $ \left( cm \right) $


- A
- B
- C
- D
Chia đa giác \[ ABCD \] thành tam giác vuông \[ AED \] , hình thang vuông \[ EDCF \] và tam giác vuông \[ FCB \] .
\[ {{S}_{AED}}=\dfrac{1}{2}AE.DE=\dfrac{1}{2}.3.4=6\left( c{{m}^{2}} \right) \]
\[ {{S}_{EDCF}}=\dfrac{\left( ED+FC \right).EF}{2}=\dfrac{\left( 4+8 \right).6}{2}=36(c{{m}^{2}}) \]
\[ {{S}_{CFB}}=\dfrac{1}{2}CF.FB=\dfrac{1}{2}.8.5=20\left( c{{m}^{2}} \right) \]
$ {{S}_{ABCD}}={{S}_{AED}}+{{S}_{EDCF}}+{{S}_{CFB}}=6+36+20=62\left( c{{m}^{2}} \right) $
Câu 6: Cho tam giác $ ABC $ với ba đường cao $ A{A}';B{B}';C{C}' $ . Gọi $ H $ là trực tâm của tam giác đó. Chọn câu đúng.
- A
- B
- C
- D

Ta có: $ {{S}_{HBC}}+{{S}_{HAC}}+{{S}_{HAB}}={{S}_{ABC}} $
$ \Rightarrow \dfrac{{{S}_{HBC}}}{{{S}_{ABC}}}+\dfrac{{{S}_{HAC}}}{{{S}_{ABC}}}+\dfrac{{{S}_{HAB}}}{{{S}_{ABC}}}=1 $
$ \Leftrightarrow \dfrac{H{A}'.BC}{A{A}'.BC}+\dfrac{H{B}'.AC}{B{B}'.AC}+\dfrac{H{C}'.BA}{C{C}'.BA}=1 $
$ \Leftrightarrow \dfrac{H{A}'}{A{A}'}+\dfrac{H{B}'}{B{B}'}+\dfrac{H{C}'}{C{C}'}=1 $ (đpcm).
Câu 7: Cho lục giác đều $ ABCDEF $ cạnh a. Gọi $ G,H,I $ tương ứng là trung điểm của các cạnh $ BC,DE,FA $ . Khi đó diện tích $ GHI $ bằng
- A
- B
- C
- D

Xét hình thang cân $ ABCF $ có $ AB=a;CF=2a $
Có $ GB=GC;IA=FI $ nên IG là đường trung bình của hình thang $ ABCF $ nên
$ GI=\dfrac{AB+FC}{2}=\dfrac{a+2a}{2}=\dfrac{3}{2}a $
Tương tự ta cũng có $ DH=\dfrac{3a}{2};HI=\dfrac{3a}{2} $
Vậy tam giác GIH là tam giác đều cạnh $ \dfrac{3a}{2}\Rightarrow {{S}_{GIH}}=\dfrac{G{{H}^{2}}\sqrt{3}}{4}=\dfrac{9{{a}^{2}}\sqrt{3}}{16} $
Câu 8: Tính diện tích của tam giác đều $ ABC $ biết chu vi tam giác $ ABC $ bằng $ 18cm $ .
- A
- B
- C
- D

Cạnh của tam giác đều là: $ AB=BC=CA=18:3=6(cm) $ .
Gọi $ AH $ là đường cao kẻ từ đỉnh $ A $ của tam giác $ ABC $ .
Khi đó $ AH $ vừa là đường cao vừa là đường trung tuyến của tam giác đều $ ABC $ .
Suy ra $ BH=HC=\dfrac{1}{2}BC=\dfrac{1}{2}.6=3(cm) $ .
Áp dụng định lí Py-ta-go trong tam giác vuông $ AHB $ ta có:
$ AH=\sqrt{A{{B}^{2}}-B{{H}^{2}}}=\sqrt{{{6}^{2}}-{{3}^{2}}}=\sqrt{27}=3\sqrt{3}(cm) $
Diện tích tam giác đều là $ {{S}_{ABC}}=\dfrac{AH.BC}{2}=\dfrac{3\sqrt{3}.6}{2}=9\sqrt{3}(c{{m}^{2}}) $ .
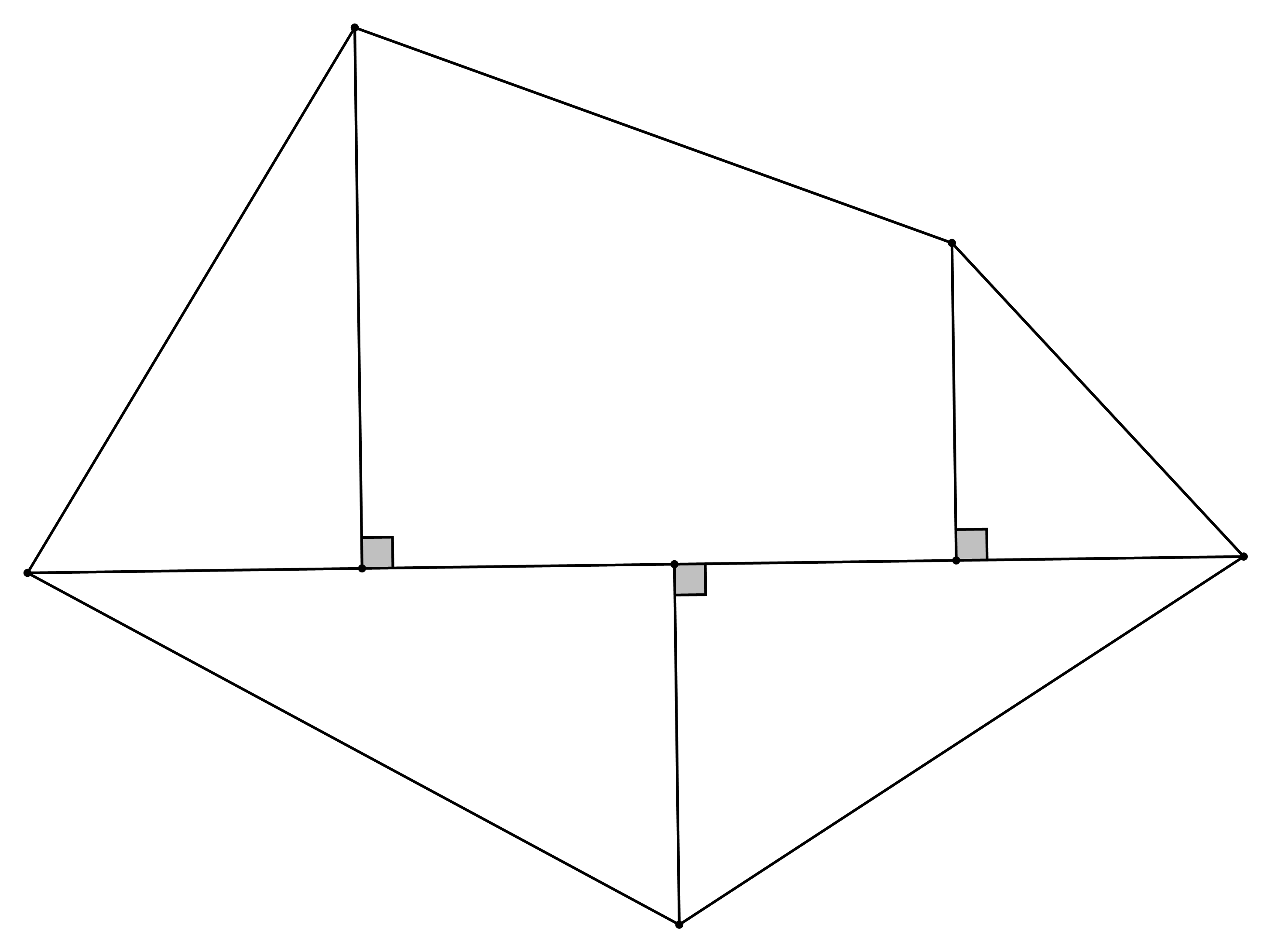
Câu 9: Đa giác $ ABCDEF $ với $ ABCD,ADEF $ là 2 hình thang, với $ AD=4cm,BC=1cm,FE=2cm,FB=3cm $ , $ FB\bot AD $ như hình vẽ. Khi đó diện tích $ ABCDEF $ bằng


- A
- B
- C
- D
Ta chia đa giác $ ABCDEF $ thành hai hình thang $ ABCD $ và $ ADEF $ .
Hình thang $ ABCD $ có cạnh đáy $ BC=1\left( cm \right) $
Đáy $ AD=AG+GD=1+3=4\left( cm \right) $
Đường cao $ BG=1\left( cm \right) $
$ {{S}_{ABCD}}=\dfrac{\left( AD+BC \right).FG}{2}=\dfrac{5}{2}(c{{m}^{2}}) $
Hình thang $ ADEF $ có đáy $ AD=4\left( cm \right) $
$ {{S}_{ADEF}}=\dfrac{\left( AD+EF \right)FG}{2}=\dfrac{\left( 4+2 \right)2}{2}=6(c{{m}^{2}}) $
$ {{S}_{ABCDEF}}={{S}_{ABCD}}+{{S}_{ADEF}}=\dfrac{5}{2}+6=\dfrac{17}{2}(c{{m}^{2}}) $
Câu 10: Cho tam giác ABC vuông tại A. Vẽ hình vuông tương ứng với mỗi cạnh trong tam giác có diện tích $ {{S}_{1}};{{S}_{2}};{{S}_{3}} $ như hình vẽ. Khi đó ta có


- A
- B
- C
- D
Ta có $ {{S}_{1}}=B{{C}^{2}};{{S}_{2}}=A{{B}^{2}};{{S}_{3}}=A{{C}^{2}} $
Có tam giác ABC vuông tại $ A\Rightarrow B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}\Rightarrow {{S}_{1}}={{S}_{2}}+{{S}_{3}} $
Câu 11: Cho hình thang $ ABCD,AB//CD $ có diện tích là $S$. Gọi $M, N$ là $2$ điểm bất kì thuộc $ AB,CD $ . Khi đó tổng diện tích $2$ tam giác $MCD$ và $NAB$ theo $S$ là
- A
- B
- C
- D

Gọi $h$ là độ dài chiều cao của hình thang hạ từ $A$ nên $h$ cũng chính là khoảng cách từ $N$ xuống $AB$, khoảng cách từ $M$ xuống $CD$
Ta có
$ \begin{array}{l} {{S}_{ABCD}}=\dfrac{\left( AB+CD \right)h}{2}=\dfrac{AB.h}{2}+\dfrac{CD.h}{2}={{S}_{ABN}}+{{S}_{MDC}} \\ \Rightarrow {{S}_{ABN}}+{{S}_{MDC}}=S \end{array} $
Câu 12: Cho hình bình hành $ ABCD $ có $ CD=4cm $ , đường cao vẽ từ $ A $ đến cạnh $ CD $ bằng $ 3cm $ . Gọi $ M $ là trung điểm của $ AB $ . Tính diện tích hình bình hành $ ABCD $ , diện tích tam giác $ ADM $ .
- A
- B
- C
- D

+ $ {{S}_{ABCD}}=AH.CD=4.3=12(c{{m}^{2}}) $ .
+ Vì $ M $ là trung điểm của $ AB $ nên $ AM=\dfrac{1}{2}AB=\dfrac{1}{2}.4=2(cm) $ .
Ta có chiều cao từ đỉnh $ D $ đến cạnh $ AM $ của tam giác $ ADM $ bằng chiều cao $ AH $ của hình bình hành.
$ \Rightarrow {{S}_{ADM}}=\dfrac{1}{2}AH.AM=\dfrac{1}{2}.3.2=3(c{{m}^{2}}) $ .
Câu 13: Một con đường cắt một đám đất hình chữ nhật với các dữ liệu được cho trên hình. Diện tích phần còn lại của đám đất là $ \left( EF//BG \right) $


- A
- B
- C
- D
Con đường hình bình hành $ EBGF $ có diện tích
$ {{S}_{EBGF}}=50.120=6000{{m}^{2}} $
Đám đất hình chữ nhật $ ABCD $ có diện tích
$ {{S}_{ABCD}}=150.120=18000{{m}^{2}} $
Diện tích phần còn lại của đám đất:
$ S={{S}_{ABCD}}-{{S}_{EBGF}}=180006000=12000{{m}^{2}} $
Câu 14: Cho tứ giác $ABCD$ và các kích thước đã cho trên hình. Diện tích tứ giác $ABCD$ bằng


- A
- B
- C
- D

Ta có $ \Delta ABC $ vuông tại B khi đó áp dụng định lý Pi-ta-go ta được
$ AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{{{8}^{2}}+{{6}^{2}}}=10 $
Quan sát hình vẽ có tam giác ADC vuông cân tại D nên
$ \begin{array}{l} A{{D}^{2}}+D{{C}^{2}}=A{{C}^{2}} \\ \Leftrightarrow 2A{{D}^{2}}=A{{C}^{2}} \\ \Rightarrow A{{D}^{2}}=\dfrac{A{{C}^{2}}}{2}=\dfrac{100}{2}=50 \\ \Rightarrow AD=5\sqrt{2} \end{array} $
Vậy diện tích $ {{S}_{ABCD}}={{S}_{ABC}}+{{S}_{ADC}}=\dfrac{1}{2}8.6+\dfrac{1}{2}.5\sqrt{2}.5\sqrt{2}=49\left( c{{m}^{2}} \right) $
Câu 15: Cho hình thoi $ ABCD $ có hai đường chéo $ AC $ và $ BD $ cắt nhau tại $ O $ . Biết $ OA=12cm $ , diện tích hình thoi $ ABCD $ là $ 168c{{m}^{2}} $ . Cạnh của hình thoi là
- A
- B
- C
- D

Ta có: $ AC=2AO=2.12=24cm $
$ {{S}_{ABCD}}=\dfrac{1}{2}BD.AC\Rightarrow BD=\dfrac{2{{S}_{ABCD}}}{AC}=\dfrac{2.168}{24}=14(cm) $
$ \Rightarrow BO=\dfrac{1}{2}BD=\dfrac{1}{2}.14=7(cm) $
Áp dụng định lí Pytago trong tam giác vuông $ AOB $ vuông tại $ O $ ta có:
$ AB=\sqrt{A{{O}^{2}}+B{{O}^{2}}}=\sqrt{{{12}^{2}}+{{7}^{2}}}=\sqrt{193}(cm) $ .
Xem thêm các bài tiếp theo bên dưới