Đồ thị phân thức b1/b1
Lưu về Facebook:
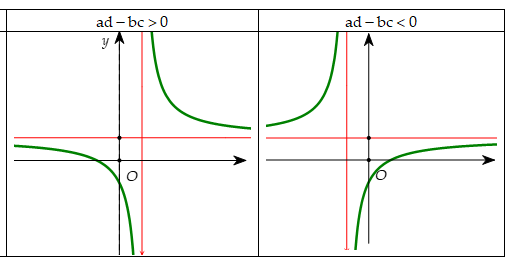
Lý thuyết về Đồ thị phân thức b1/b1
Đồ thị hàm $y=\dfrac{ax+b}{cx+d}; ad \ne cb $
Nếu đồ thị cắt $Oy$ tại $M$ thì $\dfrac{b}{d}=$ tung độ giao điểm $M$
+ giao điểm 2 đường tiệm cận là tâm đối xứng
Bài tập tự luyện có đáp án
Câu 1:  Đường cong trong hình là đồ thị của hàm số nào trong các hàm số sau?
Đường cong trong hình là đồ thị của hàm số nào trong các hàm số sau?
 Đường cong trong hình là đồ thị của hàm số nào trong các hàm số sau?
Đường cong trong hình là đồ thị của hàm số nào trong các hàm số sau?- A
- B
- C
- D
Đồ thị có tiệm cận đứng và ngang \(\Rightarrow \) Đồ thị của hàm phân thức \(y=\dfrac{x}{x-1}\)
Câu 2: Điểm $A\left( 0;1 \right)$ là tâm đối xứng của đồ thị hàm số nào dưới đây?
- A
- B
- C
- D
Tọa độ tâm đối xứng của đồ thị hàm số là giao của hai đường tiệm cận nên chọn đáp án $y=\dfrac{x+2}{x}$.
Câu 3: Điểm nào sau đây là tâm đối xứng của đồ thị hàm số $y=\dfrac{x}{1-x}$ ?
- A
- B
- C
- D
Tâm đối xứng của hàm số là giao hai đường tiệm cận nên chọn đáp án $\left( 1;-1 \right)$.
Câu 4: Để đồ thị hàm số $y=\dfrac{x+m}{x-1}$ như hình vẽ thì giá trị của $m$ bằng


- A
- B
- C
- D
Nhận thấy đồ thị cắt Oy tại $\left( 0;2 \right)\Rightarrow 2=-m\Leftrightarrow m=-2$