Định nghĩa mặt trụ
Lý thuyết về Định nghĩa mặt trụ
Định nghĩa mặt trụ:
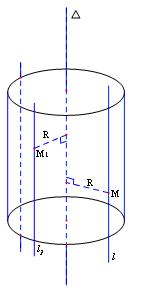
+ Cho đường thẳng $\Delta$. Xét 1 đường thẳng $l$ song song với $\Delta$, cách $\Delta$ một khoảng $R$. Khi đó: Mặt tròn xoay sinh bởi đường thẳng như thế được gọi là mặt trụ tròn xoay hoặc đơn giản là mặt trụ
- $\Delta$ gọi là trục của mặt trụ ,$l$ gọi là đường sinh và $R$ gọi là bán kính mặt trụ.Dễ thấy:
- Mặt trụ nói trên là tập hợp tất cả các điểm $M$ cách đường thẳng $\Delta$ một khoảng cố định $R$ không đổi
- Nếu ${{M}_{1}}$ là 1 điểm bất kỳ nằm trên mặt trụ thì đường thẳng ${{l}_{1}}$ đi qua ${{M}_{1}}$ và song song với $\Delta$ sẽ nằm trên mặt trụ đó.
Như vậy đường thẳng ${{l}_{1}}$ cũng là đường sinh của mặt trụ
Bài tập tự luyện có đáp án
Câu 1: Cho mặt cầu $S\left( O;R \right)$ và đường thẳng $\Delta $ cố định đi qua tâm cầu. Tập hợp tất cả các tiếp tuyến của mặt cầu song song với $\Delta $ là
- A
- B
- C
- D
Tập hợp tất cả các tiếp tuyến của mặt cầu song song với $\Delta $ là một mặt trụ có trục là $\Delta $ và bán kính bằng bán kính mặt cầu.
Câu 2: Cho mặt phẳng $\left( P \right)$ và một điểm $O\notin \left( P \right)$ cố định . Tập hợp tất cả các đường thẳng $d$ cách $O$ một khoảng không đổi và tạo với $\left( P \right)$ một góc ${{90}^{0}}$ là:
- A
- B
- C
- D
Tập hợp tất cả các đường thẳng thỏa mãn tính chất trên là một mặt trụ tròn xoay có trục là đường thẳng đi qua $O$ và vuông góc với $\left( P \right)$ , bán kính đáy của trụ là khoảng cách từ $O$ đến đường thẳng $d$
Câu 3: Cho đường thẳng $a$ cố định. Tập hợp các đường thẳng song song với $a$, cách $a$ một khoảng cố định không đổi là
- A
- B
- C
- D
Dựa vào định nghĩa sách giáo khoa, ta có đáp án là “mặt trụ”.