Xác định dấu của nghiệm phương trình bậc 2
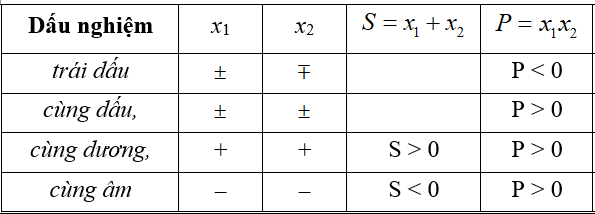
Lý thuyết về Xác định dấu của nghiệm phương trình bậc 2
Cho phương trình: ax2+bx+c=0(a≠0)ax2+bx+c=0(a≠0) . Điều kiện để phương trình có 2 nghiệm: trái dấu, cùng dấu, cùng dương, cùng âm ….
Bài tập tự luyện có đáp án
Câu 1: Cho phương trình x2−3x−7=0 có 2 nghiệm x1 và x2 . Tính x21+x22 .
- A
- B
- C
- D
Phương trình có Δ=32+4.7=37>0 .
Theo hệ thức Vi-ét ta có: {x1+x2=3x1x2=−7 .
Khi đó x21+x22=(x1+x2)2−2x1x2=32−2.(−7)=23.
Câu 2: Cho phương trình x2−5x−1=0 có 2 nghiệm x1 và x2 . Giá trị của biểu x41+x42 là
- A
- B
- C
- D
Phương trình có Δ=52+4=29>0.
Hệ thức Vi-ét: {x1+x2=5x1x2=−1.
Khi đó:
x41+x42=(x21+x22)2−2x21x22=[(x1+x2)2−2x1x2]2−2x21x22=[52−2.(−1)]2−2(−1)2=727
Câu 3: Cho phương trình: x2−3x−1=0 có 2 nghiệm x1 và x2 . Tính giá trị của biểu thức P=x1x2+1+x2x1+1 .
- A
- B
- C
- D
Phương trình có Δ=32+4=13>0
Hệ thức Vi-ét {x1+x2=3x1x2=−1.
P=x1x2+1+x2x1+1=x21+x22+(x1+x2)(x1+1)(x2+1)=(x1+x2)2+(x1+x2)−2x1x2x1x2+x1+x2+1=32+3−2.(−1)(−1)+3+1=143.
Câu 4: Cho phương trình 3x(x−2)+(x−1)(x−3)+2=0 có 2 nghiệm x1 và x2 . Tính x31+x32 .
- A
- B
- C
- D
3x(x−2)+(x−1)(x−3)+2=0⇔3x2−6x+x2−4x+3+2=0⇔4x2−10x+5=0.
Phương trình có Δ′=52−4.5=5>0.
Theo hệ thức Vi-ét ta có {x1+x2=52x1x2=54.
Khi đó x31+x32=(x1+x2)3−3x1x2(x1+x2)=(52)3−3.54.52=254.
Câu 5: Cho phương trình: √2x2−4x+1=0 có 2 nghiệm x1 và x2 . Tính giá trị của biểu thức B=x21+x22−x1x2
- A
- B
- C
- D
Phương trình có Δ′=22−√2=4−√2>0
Hệ thức Vi-ét {x1+x2=4√2=2√2x1x2=1√2=√22.
Khi đó: B=x21+x22−x1x2=(x1+x2)2−3x1x2=(2√2)2−3.√22=16−3√22.
Câu 6: Cho phương trình x2−√3x−2=0 có 2 nghiệm x1 và x2 . Giá trị của biểu thức x1x2+x2x1 là
- A
- B
- C
- D
Phương trình có: Δ=(√3)2−4.(−2)=11>0
Ta có hệ thức Vi-ét: {x1+x2=√3x1x2=−2
Khi đó: x1x2+x2x1=x21+x22x1x2=(x1+x2)2−2x1x2x1x2=3−2(−2)−2=−72.
Câu 7: Cho phương trình: 3x2−6x+2=0 có 2 nghiệm x1 và x2 . Tính giá trị của biểu thức: A=1−x1x1+1−x2x2 .
- A
- B
- C
- D
Phương trình có Δ′=(−3)2−3.2=3>0
Ta có hệ thức Vi-ét {x1+x2=2x1x2=23.
Khi đó: A=1−x1x1+1−x2x2=x1+x2−2x1x2x1x2=2−2.2323=1.
Câu 8: Cho phương trình: x(2x−1)+3x−2=0 có 2 nghiệm x1 và x2 . Tính giá trị của biểu thức: P=x21+4x1x2+x223x1x22+3x21x2.
- A
- B
- C
- D
x(2x−1)+3x−2=0⇔x2+x−1=0.
Phương trình có Δ=12−4.1.(−1)=5>0
Hệ thức Vi-ét {x1+x2=−1x1x2=−1 .
Khi đó: P=x21+4x1x2+x223x1x22+3x21x2=(x1+x2)2+2x1x23x1x2(x1+x2)=(−1)2+2(−1)3.(−1).(−1)=−13.
Câu 9: Cho phương trình: (x2+4x)(x2+4x+5)−14=0 . Tính tích các nghiệm của phương trình.
- A
- B
- C
- D
Đặt t=x2+4x ta có phương trình
t(t+5)−14=0⇔t2+5t−14=0⇔[t=−7t=2.
Với t=−7⇒x2+4x=−7⇔x2+4x+7=0 (phương trình vô nghiệm)
Với t=2 ⇒x2+4x=2⇔x2+4x−2=0(1)
Phương trình (1) có ac=−2<0
⇒ (1) có 2 nghiệm trái dấu x1 và x2
Theo hệ thức Vi-ét ta có: x1.x2=−2.
Câu 10: Cho phương trình 2(x2−1)+3x−5=0 có 2 nghiệm x1 và x2 . Tính giá trị của biểu thức P=x1x22+x21x2 .
- A
- B
- C
- D
2(x2−1)+3x−5=0⇔2x2+3x−7=0
Phương trình có Δ=32−4.2(−7)=65>0.
Theo hệ thức Vi-ét ta có: {x1+x2=−32x1x2=−72.
Khi đó P=x1x22+x21x2=x1x2(x1+x2)=(−72).(−32)=214 .
Câu 11: Phương trình x3−15x+22=0 có 1 nghiệm x=2 . Tính tổng các nghiệm còn lại của phương trình.
- A
- B
- C
- D
x3−15x+22=0⇔(x−2)(x2+2x−11)=0⇔[x=2x2+2x−11=0(1)
Phương trình (1) luôn có 2 nghiệm x1;x2
Theo hệ thức Vi-ét ta có: x1+x2=−2.
Câu 12: Cho phương trình: x2−(m+2)x+2m=0 ( m là tham số) có 2 nghiệm x1 và x2 . Tính theo m giá trị của biểu thức P=(x1−x2)2 .
- A
- B
- C
- D
Phương trình có Δ=(m+2)2−8m=m2−4m+4=(m−2)2≥0
Hệ thức Vi-ét: {x1+x2=m+2x1x2=2m.
P=(x1−x2)2=(x1+x2)2−4x1x2=(m+2)2−4.2m=(m−2)2
Câu 13: Cho phương trình: x4−3x3+2x2−3x+1=0 có 2 nghiệm x1 và x2 . Tính giá trị của biểu thức: A=x1+x2−x1x2 .
- A
- B
- C
- D
x4−3x3+2x2−3x+1=0⇔(x4+x2)−(3x3+3x)+(x2+1)=0⇔x2(x2+1)−3x(x2+1)+(x2+1)=0⇔(x2+1)(x2−3x+1)=0⇔x2−3x+1=0(1)
Phương trình (1) có Δ=32−4=5>0
Hệ thức Vi-ét {x1+x2=3x1x2=1.
Khi đó: A=x1+x2−x1x2=3−1=2.
Xem thêm các bài tiếp theo bên dưới