Thể tích của khối tròn xoay

Cho hàm số $y = f(x)$ liên tục, không âm trên $[a; b]$. Hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$, trục hoành và hai đường thẳng $x = a, x=b$ quay quanh trục hoành tạo nên một khối tròn xoay có thể tích được tính bởi công thức $$V=\pi \int\limits_{a}^{b}{f^2(x)dx}.$$

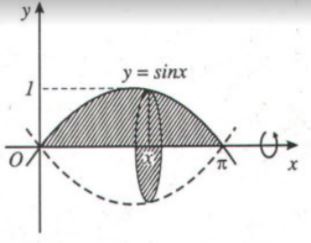
Ví dụ. Cho hình phẳng giới hạn bởi đường cong $y=\sin{x}$, trục hoành và hai đường thẳng $x=0, x=\pi$. Tính thể tích khối tròn xoay thu được khi quay hình này xung quanh trục $Ox$.

Giải. Áp dụng công thức$V=\pi \displaystyle\int\limits_{a}^{b}{f^2(x)dx}$ ta có

$$V=\pi \int\limits_{0}^{\pi }{\sin^{2}xdx}=\dfrac{\pi }{2} \int\limits_{0}^{\pi }{(1-\cos{2x})dx}=\dfrac{\pi }{2}\left.\left( x-\dfrac{1}{2}\sin 2x \right)\right|_{0}^{\pi}=\dfrac{\pi ^ 2}{2}$$