Biểu diễn hình học của số phức
Lý thuyết về Biểu diễn hình học của số phức
Trong hệ trục tọa độ Oxy
- Với mỗi z=a+bi(a,b∈R) ta đặt tương ứng điểm M(a;b)
- Với mỗi M(a;b) là điểm biểu diễn một số phức z=a+bi.
- Ox được gọi là trục thực
- Oy được gọi là trục ảo
Vectơ →u có tọa độ (a;b) biểu diễn z=a+bi.
M biểu diễn số phức z cũng có nghĩa là vectơ →OM biểu diễn số phức đó.
Nếu →u,→u′ theo thứ tự biểu diễn các số phức z,z′ thì:
- →u+→u′ biểu diễn số phức z+z′.
- →u−→u′ biểu diễn số phức z−z′.
Bài tập tự luyện có đáp án
Câu 1: Trong các khẳng định sau, khẳng định nào không đúng:
Trong các khẳng định sau, khẳng định nào không đúng:
- A
- B
- C
- D
Nếu tổng của 2 số phức là số thực thì cả 2 số ấy đều là số thực là sai chẳng hạn:
z1=3+i,z2=2−iz1+z2=5
Câu 2: Điểm biểu diễn số phức z=2−2i thuộc đường thẳng nào trong các đường thẳng sau?
- A
- B
- C
- D
Thay tọa độ điểm M(2;−2) biểu diễn số phức z vào các đường thẳng thì thỏa mãn phương trình đường thẳng y=−x
Câu 3: Trong mặt phẳng phức, →OM(3;−5) biểu diễn số phức
- A
- B
- C
- D
→OM(3;−5)biểu diễn số phức 3−5i
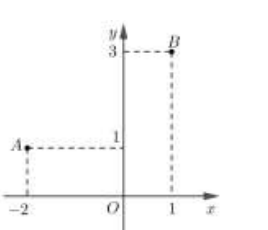
Câu 4:  Trong mặt phẳng Oxy, cho các điểm A, B như hình vẽ bên. Trung điểm của đoạn thẳng AB biểu diễn số phức
Trong mặt phẳng Oxy, cho các điểm A, B như hình vẽ bên. Trung điểm của đoạn thẳng AB biểu diễn số phức
 Trong mặt phẳng Oxy, cho các điểm A, B như hình vẽ bên. Trung điểm của đoạn thẳng AB biểu diễn số phức
Trong mặt phẳng Oxy, cho các điểm A, B như hình vẽ bên. Trung điểm của đoạn thẳng AB biểu diễn số phức- A
- B
- C
- D
Phương pháp:
+ Số phức z=a+bi(a,b∈Z) được biểu diễn bởi điểm M(a;b) trên mặt phẳng xOy.
+ Tọa độ trung điểm I của AB là: {x1=xA+xB2x2=yA+yB2
Cách giải:
Dựa vào hình vẽ ta thấy: A(−2;1),B(1;3)⇒M(−12;2)⇒z=−12+2i
Câu 5:  Trong hình vẽ bên, điểm M biểu diễn số phức z. Số phức ˉz là
Trong hình vẽ bên, điểm M biểu diễn số phức z. Số phức ˉz là
 Trong hình vẽ bên, điểm M biểu diễn số phức z. Số phức ˉz là
Trong hình vẽ bên, điểm M biểu diễn số phức z. Số phức ˉz là- A
- B
- C
- D
z=2+i⇒¯z=2−i
Câu 6:  Điểm nào trong hình vẽ dưới đây là điểm biễu diễn của số phức z=(1+i)(2−i)?
Điểm nào trong hình vẽ dưới đây là điểm biễu diễn của số phức z=(1+i)(2−i)?
 Điểm nào trong hình vẽ dưới đây là điểm biễu diễn của số phức z=(1+i)(2−i)?
Điểm nào trong hình vẽ dưới đây là điểm biễu diễn của số phức z=(1+i)(2−i)?- A
- B
- C
- D
Ta có z=2−i+2i−i2=3+i⇒ số phức z biểu diễn Q(3;1).
Câu 7: Trong mặt phẳng Oxy, hai điểm biểu diễn hai số phức z và −z :
- A
- B
- C
- D
Gọi z=a+bi(a,b∈R) vậy tọa độ điểm biểu diễn của z là (a;b)
Có −z=−a−bi vậy tọa độ điểm biểu diễn của −z là (−a;−b)
Do (a;b)và (−a;−b) đối xứng nhau qua gốc tọa độ O, nên hai điểm biểu diễn hai số phức z và −z đối xứng nhau qua gốc tọa độ.
Câu 8: Điểm M trong hình vẽ bên là điểm biểu diễn số phức


- A
- B
- C
- D
Điểm M(−2;1) là điểm biểu diễn số phức z=−2+i .
Câu 9: Cho số phức z=1+2i. Khi đó điểm biểu diễn số phức nằm trên đường thẳng
- A
- B
- C
- D
Với z=1+2i⇒điểm biểu diễn số phức z là điểm M(1;2) thuộc đường y=x+1.
Câu 10: Biết điểm M(−1;2) là điểm biểu diễn số phức z . Vậy z bằng
- A
- B
- C
- D
Số phức z=a+bi có điểm biểu diễn là M(a;b) nên chọn đáp án z=−1+2i
Câu 11: Số phức z nào sau đây có môđul bằng môđul của số phức có điểm biểu diễn là M(1;−3)
- A
- B
- C
- D
Ta có số phức có điểm biểu diễn M(1;−3) là z′=1−3i⇒|z′|=√10
Thấy trong các phương án thì chỉ có |√6+2i|=√6+4=√10
Vậy z=√6−2i.
Câu 12: Trên mặt phẳng tọa độ, điểm biểu diễn số phức z=−1+2i là điểm nào dưới đây?
- A
- B
- C
- D
Điểm biểu diễn số phức z=−1+2i là điểm P(−1;2) .
Câu 13: Biết A,B là điểm biểu diễn số phức z=−i,z=3i. Độ dài AB bằng
- A
- B
- C
- D
Ta có A(0;−1),B(0;3)⇒AB=4
Câu 14: Điểm M(1;−3) trên mặt phẳng tọa độ biểu diễn số phức
- A
- B
- C
- D
Điểm M(1;−3) trên mặt phẳng tọa độ biểu diễn số phức 1−3i .
Câu 15: Cho số phức z=2+3i . Tọa độ điểm biểu diễn số phức ¯z là
- A
- B
- C
- D
Số phức ¯z=2−3i⇒Tọa độ điểm biểu diễn số phức ¯z là (2;−3).
Câu 16: Điểm nào trong hình vẽ bên là điểm biểu diễn của số phức z=−1+2i?


- A
- B
- C
- D
Vì z=−1+2i nên điểm biểu diễn số phức z có tọa độ (−1;2) , đối chiếu hình vẽ ta thấy đó là điểm Q .
Câu 17: Cho số phức z=1−4i. Số phức đối của z có điểm biểu diễn là:
- A
- B
- C
- D
Số phức đối của z là −1+4i⇒(−1;4) là điểm biểu diễn cần tìm
Câu 18: Số phức nào sau đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình bên ?


- A
- B
- C
- D
Điểm M có tọa độ là (−2;1) do đó M biểu diễn số phức z3=−2+i
Câu 19: Cho số phức z1=1−2i, z2=−3+i. Tìm điểm biểu diễn của số phức z=z1+z2 trên mặt phẳng tọa độ.
- A
- B
- C
- D
Ta có z=z1+z2=−2−i
Câu 20: Trong mặt phẳng phức Oxy, cho số phức z=a+bi,(a,b∈R) . Khẳng định sai là:
- A
- B
- C
- D
“Điểm biểu diễn số phức −a+bi đối xứng với điểm biểu diễn z qua trục hoành” là khẳng định sai vì hai điểm này đối xứng nhau qua trục tung.
Câu 21: Số phức nào dưới đây có điểm biểu diễn thuộc đường tròn x2+y2=4.
- A
- B
- C
- D
Thay tọa độ các điểm biểu diễn các số phức trong các phương án, điểm nào thỏa mãn phương trình đường tròn thì chọn
Ta thấy điểm (√2;−√2) thuộc đường tròn nên chọn số phức z=√2−√2i
Câu 22: Biết điểm M biểu diễn số phức z=1+i. Độ dài →OM bằng
- A
- B
- C
- D
Ta có |→OM|=|z|=√2
Câu 23: Nếu →OM=(1;−2) thì điểm M là điểm biểu diễn của số phức
- A
- B
- C
- D
→OM=(1;−2)⇒M(1;−2) hay điểm M biểu diễn số phức z=1−2i
Câu 24: Điểm M trong hình vẽ là điểm biểu thị cho số phức


- A
- B
- C
- D
Ta có điểm M(−2;3) ⇒ Điểm M biểu diễn số phức −2+3i
Câu 25: Cho các điểm M,N,P lần lượt biểu diễn các số phức z1=−2i,z2=−i,z3=5i . Trong các khẳng định sau, khẳng định đúng là
- A
- B
- C
- D
Thấy 3 số phức z không có phần thực nên 3 điểm M,N,P thuộc Oy nên khẳng định “Các điểm M,N,P thẳng hàng” đúng.
Xem thêm các bài tiếp theo bên dưới