Thế tích khối chóp
Lý thuyết về Thế tích khối chóp
Thể tích của 1 khối chóp bắng một phần ba tích số của mặt đáy và chiều cao khối chóp đó
Ví dụ. Tính thể tích của khối tứ diện đều có cạnh bằng a
Giải:
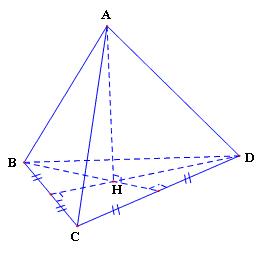
Xem tứ diện đều ABCD cạnh a như hình chóp có đỉnh A và đáy là tam giác đều BCD. Diện tích mặt đáy là: SBCD=√34a2.
Gọi AH là chiều cao của hình chóp A.BCD thì H là tâm của tam giác đều BCD. Suy ra chiều cao hình chóp là: h=AH=√AB2−BH2=√a2−a23=a√2√3.
Từ đó suy ra khối tứ diện ABCD có thể tích là:V=13SBCD.h=a3√212
Bài tập tự luyện có đáp án
Câu 1: Cho hình chóp S.ABCD có đáy là hình chữ nhật, SD vuông góc với đáy. Biết SD=AB=a, BC=b. Thể tích khối chóp S.ABCD là:
- A
- B
- C
- D
Câu 2: Cho khối chóp S.ABC. Khi tăng cạnh đáy của ΔABC lên hai lần và giảm chiều cao ứng với đáy đi hai lần thì thể tích của khối chóp S.ABC
- A
- B
- C
- D
Câu 3: Hình hộp chữ nhật ABCD.A′B′C′D′ có thể tích là V, khẳng định nào sau đây là sai:
- A
- B
- C
- D
Câu 4: Trong các mệnh đề sau, mệnh đề nào sai?
- A
- B
- C
- D
Câu 5: Cho hình lăng trụ tứ giác ABCD.A′B′C′D′ và điểm M bất kì thuộc (ABCD) . Tỉ số thể tích của lăng trụ và hình chóp MA′B′C′D′ là
- A
- B
- C
- D

Gọi h,S lần lượt là chiều cao và diện tích đáy của hình lăng trụ.
Ta có VABCD.A′B′C′D′=h.S
Vì điểm M bất kì thuộc (ABCD)//(A′B′C′D′)
⇒VMA′B′C′D′=13h.S⇒VABCD.A′B′C′D′VMA′B′C′D′=3
Câu 6: Cho ΔABC cố định và điểm M∉(ABC) thay đổi. Thể tích khối chóp MABC thay đổi nếu:
- A
- B
- C
- D
Câu 7: Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy là a, chiều cao hình chóp gấp 3 lần cạnh đáy. Thể tích hình chóp S.ABCD là
- A
- B
- C
- D
Câu 8: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA⊥(ABCD), ^SBA=450. Thể tích hình chóp S.ABCD là
- A
- B
- C
- D

⇒SA=AB=a
⇒VS.ABCD=13SA.SABCD=a33
Câu 9: Cho hình chóp S.ABCD có đáy là hình vuông. Gọi V là thể tích khối chóp S.ABCD. Khi đó thể tích S.ABC bằng
- A
- B
- C
- D
Ta có VS.ABC=13hSABC=13h12SABCD=V2
(h là độ dài đường cao của hình chóp).
Câu 10: Khi chiều cao của hình chóp tứ giác đều tăng lên hai lần và độ dài cạnh đáy giảm đi hai lần thì thể tích hình chóp
- A
- B
- C
- D
Gọi a là độ dài cạnh đáy, h là chiều cao của hình chóp.
Khi đó ta có thể tích ban đầu là V1=13a2h
Khi tăng chiều cao của hình chóp lên hai lần và giảm độ dài cạnh đáy đi hai lần thì được thể tích mớiV2=13.2h.(a2)2=13h.a22=12V1.
Vậy thể tích mới giảm đi 2 lần.
Xem thêm các bài tiếp theo bên dưới