Định nghĩa hai tam giác bằng nhau
Lý thuyết về Định nghĩa hai tam giác bằng nhau
1. Định nghĩa
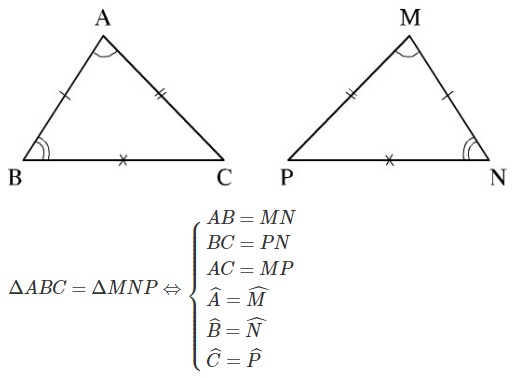
Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với ba cạnh của tam giác kia.
2. Kí hiệu
Để kí hiệu sự bằng nhau của tam giác $ABC$ và tam giác $MNP$ ta viết: $∆ABC= ∆MNP$.
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác ABC, biết rằng $ \widehat{A}:\widehat{B}:\widehat{C}=2:3:4. $ Khi đó số đo góc $ A $ và góc $ C $ là:
- A
- B
- C
- D
$ \begin{array}{l} \widehat{A}:\widehat{B}:\widehat{C}=2:3:4\Rightarrow \dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{2+3+4}=\dfrac{{{180}^{0}}}{9}={{20}^{0}}. \\ \Rightarrow \widehat{A}={{40}^{0}};\,\,\widehat{B}={{60}^{0}};\,\,\widehat{C}={{80}^{0}}. \end{array} $
Câu 2: Cho $ \Delta ABC $ có $ \widehat{B} $ và $ \widehat{C} $ là các góc nhọn. Qua B kẻ đoạn thẳng BD vuông góc với AC $ \left( D\in AC \right) $ . Qua C kẻ đoạn thẳng CE vuông góc với AB $ \left( E\in AB \right). $ Gọi H là giao điểm của BD và CE. Mối quan hệ giữa $ \widehat{A} $ và $ \widehat{DHE} $ là:
- A
- B
- C
- D

$ \Delta ACE $ có: $ \widehat{A}+\widehat{ACE}={{90}^{0}} $ (Vì $ CE\bot AB $ ).
$ \widehat{HCD} $ có: $ {{\widehat{H}}_{1}}+\widehat{ACE}={{90}^{0}} $ (Vì $ BD\bot AC $ ).
$ \Rightarrow \widehat{A}={{\widehat{H}}_{1}}. $
Ta lại có: $ {{\widehat{H}}_{1}}+{{\widehat{H}}_{2}}={{180}^{0}} $ (kề bù).
Do đó: $ \widehat{A}+{{\widehat{H}}_{2}}={{180}^{0}}. $
Câu 3: Cho tam giác ABC vuông tại A. Trên nửa mặt phẳng bờ BC có chứa A, vẽ các tia Bx và Cy cùng vuông góc với BC. Khi đó $ \widehat{xBA}+\widehat{yCA} $ bằng:
- A
- B
- C
- D

Ta có: $ \widehat{xBA}+\widehat{yCA}=\left( \widehat{xBC}-\widehat{ABC} \right)+\left( \widehat{yCB}-\widehat{ACB} \right) $ $ =\left( \widehat{xBC}+\widehat{yCB} \right)-\left( \widehat{ABC}+\widehat{ACB} \right) $ . (1)
Vì Bx và Cy cùng vuông góc với BC nên $ \widehat{xBC}+\widehat{yCB}={{90}^{0}}+{{90}^{0}}={{180}^{0}}. $ (2)
Vì $ \Delta ABC $ vuông tại A $ \Rightarrow \widehat{ABC}+\widehat{ACB}={{90}^{0}} $ . (3)
Từ (1) (2) và (3) $ \Rightarrow \,\,\,\widehat{xBA}+\widehat{yCA}={{180}^{o}}-{{90}^{0}}={{90}^{o}} $ .
Câu 4: Tam giác ABC có $ \widehat{A} > \widehat{B}. $ Khẳng định nào sau đây là đúng ?
- A
- B
- C
- D
Theo đề bài, ta có: $ \widehat{B} < \widehat{A}. $ (1)
Hiển nhiên: $ \widehat{B} < \widehat{B}+\widehat{C}. $ (2)
Cộng theo từng về (1) và (2), ta có: $ 2\widehat{B} < \widehat{A}+\widehat{B}+\widehat{C}={{180}^{0}}. $
Vậy $ \widehat{B} < {{90}^{0}}. $
Câu 5: Chọn đáp án đúng. Cho $ \Delta MNP=\Delta ABC $ có $ MN=6cm\,;AC=7cm\,;NP=10cm $ . Khi đó:
Cho $ \Delta MNP=\Delta ABC $ có $ MN=6cm\,;AC=7cm\,;NP=10cm $ . Khi đó:
- A
- B
- C
- D
$ \Delta MNP=\Delta ABC $
$ \Rightarrow \,\,MN=AB\,;\,MP=AC\,;\,NP=BC $
Mà $ MN=6cm\,;AC=7cm\,;NP=10cm $
$ \Rightarrow \,\,AB=6cm,\,\,MP=7cm,\,BC=10cm $ .
Câu 6: Cho $ \Delta ABC=\Delta DEF $ , biết $ AB=6cm\,;\,BC=10cm\,;DF=14cm. $ Chu vi tam giác DEF là:
- A
- B
- C
- D
$ \Delta ABC=\Delta DEF\, $
$ \Rightarrow \,\,AB=DE\,=6cm\,\,; $ $ AC=DF=14cm\,; $ $ BC=EF=10cm. $
Chu vi tam giác DEF là: $ DE+DF+EF=6+14+10=30\,(cm). $
Câu 7: Cho $ \Delta ABC=\Delta D\text{EF} $ có $ \widehat{A}={{70}^{o}},\,\,\widehat{E}={{50}^{o}} $ . Tính số đo góc $ \widehat{C} $ .
- A
- B
- C
- D
Ta có $ \Delta ABC=\Delta D\text{EF}\Rightarrow \left\{ \begin{array}{l} \widehat{A}=\widehat{D} \\ \widehat{B}=\widehat{E} \\ \widehat{C}=\widehat{F} \end{array} \right. $
Mặt khác $ \widehat{A}+\widehat{B}+\widehat{C}=\widehat{A}+\widehat{E}+\widehat{C}={{180}^{o}}\Rightarrow \widehat{C}={{60}^{o}} $
Câu 8: Cho $ \Delta EFM=\Delta KPN $ và $ \widehat{E}=\widehat{K}={{90}^{o}} $ . Khi đó, tỉ số diện tích của tam giác EFM và diện tích tam giác KPN bằng:
- A
- B
- C
- D
Vì $ \Delta EFM=\Delta KPN $ nên $ EF=KP\,;\,EM=KN\,;\,FM=PN $ .
Tam giác EFM có $ \widehat{E}={{90}^{o}} $ $ \Rightarrow \,\Delta EFM $ vuông tại E $ \Rightarrow \,{{S}_{EFM}}=\dfrac{1}{2}EF.EM $ .
Tam giác KPN có $ \widehat{K}={{90}^{o}} $ $ \Rightarrow \,\Delta KPN $ vuông tại K $ \Rightarrow \,{{S}_{KPN}}=\dfrac{1}{2}KP.KN $ .
Khi đó: $ \dfrac{{{S}_{EFM}}}{{{S}_{KPN}}}=\dfrac{EF.EM}{KP.KN}=\dfrac{KP.KN}{KP.KN}=1. $
Câu 9: Cho $ \Delta ABC=\Delta KPN $ , biết rằng chu vi tam giác KPN bằng 30cm; $ AB=9cm\,;\,KN=14cm $ . Độ dài cạnh BC là:
- A
- B
- C
- D
Vì $ \Delta ABC=\Delta KPN $ nên $ AB=KP=9cm\,; $ $ AC=KN=14cm\,;\,BC=PN. $
Vì chu vi tam giác KPN bằng 30cm nên $ KP+KN+PN=30\,(cm) $
$ \Rightarrow \,PN=30-(KP+KN)=30-(9+14)=7\,(cm). $
Vậy $ BC=PN=7cm. $
Câu 10: Cho $ \Delta ABC=\Delta DEF $ có $ \widehat{C}={{60}^{0}},\widehat{B}={{55}^{0}} $ . Số đo góc D là:
- A
- B
- C
- D
$ \Delta ABC=\Delta DEF\,\Rightarrow \,\,\widehat{A}=\widehat{D}\,;\,\widehat{B}=\widehat{E}={{55}^{o}}\,;\,\widehat{C}=\widehat{F}={{60}^{o}} $ .
Xét tam giác DEF có $ \widehat{D}+\widehat{E}+\widehat{F}={{180}^{o}} $
$ \Rightarrow \,\,\widehat{D}={{180}^{o}}-\left( \widehat{E}+\widehat{F} \right)={{180}^{o}}-\left( {{55}^{o}}+{{60}^{o}} \right)={{65}^{o}} $ .
Câu 11: Cho $ \Delta ABC=\Delta MNP $ , biết $ \widehat{B}={{70}^{0}}\,;\,\widehat{P}={{40}^{0}} $ . Khi đó tam giác MNP là:
- A
- B
- C
- D
Vì $ \Delta ABC=\Delta MNP $ $ \Rightarrow \,\,\widehat{A}=\widehat{M}\,;\,\widehat{B}=\widehat{N}\,={{70}^{o}};\,\widehat{C}=\widehat{P}={{40}^{o}} $ .
Xét tam giác MNP có: $ \widehat{M}+\widehat{N}+\widehat{P}={{180}^{o}} $
$ \Rightarrow \,\,\widehat{M}={{180}^{o}}-\left( \widehat{N}+\widehat{P} \right)={{180}^{o}}-\left( {{70}^{o}}+{{40}^{o}} \right)={{70}^{o}} $
Vậy tam giác MNP có $ \widehat{M}=\widehat{N}={{70}^{o}} $ .
Câu 12: Cho $ \Delta ABC=\Delta DEG $ biết $ \widehat{A}=\widehat{B}=2\widehat{C} $ . Số đo $ \widehat{E} $ là
- A
- B
- C
- D
Ta có $ \widehat{A}+\widehat{B}+\widehat{C}={{180}^{o}} $ mà $ \widehat{A}=\widehat{B}=2\widehat{C} $ nên $ \left\{ \begin{array}{l} \widehat{A}={{72}^{o}} \\ \widehat{B}={{72}^{o}} \\ \widehat{C}={{36}^{o}} \end{array} \right. $
Mà $ \Delta ABC=\Delta DEG\Rightarrow \widehat{E}=\widehat{B}={{72}^{o}} $
Câu 13: Cho $ \Delta ABC=\Delta MNP $ có $ AC=8cm,MN=6cm,BC=9cm $ . Chu vi của tam giác $ MNP $ bằng
- A
- B
- C
- D
Do $ \Delta ABC=\Delta MNP\Rightarrow \left\{ \begin{array}{l} AB=MN \\ BC=NP \\ AC=MP \end{array} \right. $
Chu vi tam giác $ MNP $ là $ MN+NP+MP=MN+BC+AC=6+9+8=23\,cm $
Câu 14: Cho tam giác ABC bằng một tam giác có ba đỉnh P, E, Q. Biết rằng $ AB=QP\,;\,BC=E\,Q $ . Hệ thức bằng nhau giữa hai tam giác đó là :
Hệ thức bằng nhau giữa hai tam giác đó là :
- A
- B
- C
- D
Vì $ AB=QP\,;\,BC=E\,Q $ và $ \Delta ABC $ bằng một tam giác có ba đỉnh P, E, Q nên AC = PE.
Khi đó hai tam giác bằng nhau theo thứ tự đỉnh tương ứng là: $ \Delta ABC=\Delta PQE $ .
Câu 15: Cho $ \Delta PQ\text{R}=\Delta SIK $ có $ \widehat{P}={{90}^{o}},\,\,\widehat{I}={{50}^{o}} $ . Tính số đo góc $ \widehat{R} $ .
- A
- B
- C
- D
Ta có $ \Delta PQ\text{R}=\Delta SIK\Rightarrow \left\{ \begin{array}{l} \widehat{P}=\widehat{S} \\ \widehat{Q}=\widehat{I} \\ \widehat{R}=\widehat{K} \end{array} \right. $
Mặt khác $ \widehat{P}+\widehat{Q}+\widehat{R}=\widehat{P}+\widehat{I}+\widehat{R}={{180}^{o}}\Rightarrow \widehat{R}={{40}^{0}} $
Câu 16: Cho \[ \Delta ABC=\Delta MNP \] , biết \[ \widehat{B}={{50}^{0}},\widehat{P}={{85}^{0}} \] .
Chọn phương án sai.
- A
- B
- C
- D
$ \Delta ABC=\Delta MNP $
$ \Rightarrow \,\widehat{A}=\widehat{M}\,;\,\widehat{B}=\widehat{N}\,={{50}^{o}}\,;\,\widehat{C}=\widehat{P}={{85}^{o}} $
Xét tam giác ABC có: $ \widehat{A}+\widehat{B}+\widehat{C}={{180}^{o}} $
$ \Rightarrow \,\widehat{A}={{180}^{o}}-\left( \widehat{B}+\widehat{C} \right)={{180}^{o}}-({{50}^{o}}+{{85}^{o}})={{45}^{o}} $ .
$ \Rightarrow \,\widehat{M}=\widehat{A}={{45}^{o}}. $
Câu 17: Cho $ \Delta ABC=\Delta KPN $ . Khi đó, tỉ số chu vi tam giác ABC và chu vi tam giác KPN bằng:
- A
- B
- C
- D
$ \Delta ABC=\Delta KPN $ $ \Rightarrow \,AB=KP\,;\,AC=KN\,;\,BC=PN $ .
Chu vi tam giác ABC là: $ {{C}_{ABC}}=AB+AC+BC $ .
Chu vi tam giác KPN là: $ {{C}_{KPN}}=KP+KN+PN $ .
Do đó: $ \dfrac{{{C}_{ABC}}}{{{C}_{KPN}}}=\dfrac{AB+AC+BC}{KP+KN+PN}=1. $
Câu 18: Cho $ \Delta ABC=\Delta DEF $ , tính chu vi tam giác $ DEF $ , biết rằng $ AB=5cm,BC=7cm,DF=6cm $ .
- A
- B
- C
- D
Ta có $ \Delta ABC=\Delta DEF\Rightarrow \left\{ \begin{array}{l} AC=DF \\ AB=DE \\ BC=\text{EF} \end{array} \right. $
Chu vi tam giác $ DEF $ là $ DF+DE+F\text{E}=DF+AB+BC=6+5+7=18\,\,cm $
Câu 19: Cho $ \Delta ABC=\Delta MNP $ , biết $ \widehat{A}={{60}^{0}}\,;\,\widehat{P}={{30}^{0}} $ . Khi đó tam giác ABC là:
- A
- B
- C
- D
Vì $ \Delta ABC=\Delta MNP $ $ \Rightarrow \,\,\widehat{A}=\widehat{M}={{60}^{o}}\,;\,\widehat{B}=\widehat{N}\,;\,\widehat{C}=\widehat{P}={{30}^{o}} $ .
Xét tam giác ABC có: $ \widehat{A}+\widehat{B}+\widehat{C}={{180}^{o}} $
$ \Rightarrow \,\,\widehat{B}={{180}^{o}}-\left( \widehat{A}+\widehat{C} \right)={{180}^{o}}-\left( {{60}^{o}}+{{30}^{o}} \right)={{90}^{o}} $
$ \Rightarrow \,\Delta ABC $ vuông tại B.
Xem thêm các bài tiếp theo bên dưới