Định nghĩa Cho hai điểm cố định $F_1$ và $F_2,$ với $F_1F_2
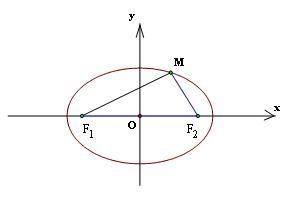
Lý thuyết về Định nghĩa Cho hai điểm cố định $F_1$ và $F_2,$ với $F_1F_2
Định nghĩa
Cho hai điểm cố định $F_1$ và $F_2,$ với $F_1F_2=2c(c>0)$
Đường elip ( còn gọi là elip ) là tập hợp các điểm M sao cho $MF_1+MF_2=2a$, trong đó $a$ là số cho trước lớn hơn $c$.
Hai điểm $F_1$ và $F_2$ gọi là các tiêu điểm của các elip. Khoảng cách 2c được gọi là tiêu cự của elip
Bài tập tự luyện có đáp án
Câu 1: Cho hai điểm cố định $ {{F}_{1}},{{F}_{2}} $ và một độ dài không đổi $ 2a $ lớn hơn $ {{F}_{1}}{{F}_{2}} $ . Elip là tập hợp điểm M trong mặt phẳng thỏa mãn điều kiện :
- A
- B
- C
- D
Theo định nghĩa sgk trang 85 : Cho hai điểm cố định $ {{F}_{1}},{{F}_{2}} $ và một độ dài không đổi $ 2a $ lớn hơn $ {{F}_{1}}{{F}_{2}} $ . Elip là tập hợp điểm M trong mặt phẳng sao cho $ {{F}_{1}}M+{{F}_{2}}M=2a $ .
Câu 2: Cho elip $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $ và tọa độ các tiêu điểm $ {{F}_{1}}\left( -c;0 \right),{{F}_{2}}\left( c;0 \right) $ khẳng định nào sau đây sai ?
- A
- B
- C
- D
Khẳng định sai là: $ {{a}^{2}}={{b}^{2}}-{{c}^{2}} $
Câu 3: Cho elip $ \left( E \right) $ có phương trình $ \dfrac{{{x}^{2}}}{81}+\dfrac{{{y}^{2}}}{64}=1 $ . Độ dài trục lớn của $ \left( E \right) $ bằng
- A
- B
- C
- D
$ \left( E \right):\dfrac{{{x}^{2}}}{81}+\dfrac{{{y}^{2}}}{64}=1 $ .
$ \Rightarrow {{a}^{2}}=81\Rightarrow a=9\Rightarrow 2a=18 $ .
Độ dài trục lớn của $ \left( E \right) $ bằng $ 18 $ .
Câu 4: Trong mặt phẳng $ Oxy $ , phương trình chính tắc của elip có độ dài trục lớn bằng 8, độ dài trục nhỏ bằng 6 là:
- A
- B
- C
- D
Độ dài trục lớn $ 2a\,=\,8\,\Rightarrow \,a\,=\,4 $ .
Độ dài trục nhỏ $ 2b\,=\,6\,\Rightarrow \,b\,=\,3 $ .
Vậy phương trình elip là: $ \dfrac{{{x}^{2}}}{16}\,+\,\dfrac{{{y}^{2}}}{9}\,=\,1 $ .