Tổng bình phương hai cạnh và độ dài đường trung tuyến của tam giác
Lý thuyết về Tổng bình phương hai cạnh và độ dài đường trung tuyến của tam giác
Tổng bình phương hai cạnh và độ dài đường trung tuyến của tam giác
Cho tam giác $ABC$. Gọi $m_a,m_b,m_c$ là độ dài các đường trung tuyến lần lượt ứng với các cạnh $BC=a,CA=b,AC=c$. Ta có các công thức sau là công thức trung tuyến:
${{m}_{a}}^{2}=\dfrac{{{b}^{2}}+{{c}^{2}}}{2}-\dfrac{{{a}^{2}}}{4};{{m}_{b}}^{2}=\dfrac{{{a}^{2}}+{{c}^{2}}}{2}-\dfrac{b}{4};{{m}_{c}}^{2}=\dfrac{{{a}^{2}}+{{b}^{2}}}{2}-\dfrac{{{c}^{2}}}{4}$
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác \[ ABC \] có độ dài các cạnh là $a, b, c$ và thoả mãn \[ {{b}^{2}}+{{c}^{2}}-{{a}^{2}}=\sqrt{3}bc \] . Tính số đo của góc A.
- A
- B
- C
- D
Ta có: $ \cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}=\dfrac{\sqrt{3}bc}{2bc}=\dfrac{\sqrt{3}}{2}\Rightarrow A={{30}^{0}} $
Câu 2: Gọi $ S=m_{a}^{2}+m_{b}^{2}+m_{c}^{2} $ là tổng bình phương độ dài ba trung tuyến của tam giác $ ABC $ . Trong các mệnh đề sau mệnh đề nào đúng ?
- A
- B
- C
- D
Ta có: $ S=m_{a}^{2}+m_{b}^{2}+m_{c}^{2}=\dfrac{{{b}^{2}}+{{c}^{2}}}{2}-\dfrac{{{a}^{2}}}{4}+\dfrac{{{a}^{2}}+{{c}^{2}}}{2}-\dfrac{{{b}^{2}}}{4}+\dfrac{{{a}^{2}}+{{b}^{2}}}{2}-\dfrac{{{c}^{2}}}{4}=\dfrac{3}{4}({{a}^{2}}+{{b}^{2}}+{{c}^{2}}). $
Câu 3: Cho $ \Delta ABC $ có $ a=6,b=8,c=10. $ Diện tích $ S $ của tam giác trên là:
- A
- B
- C
- D
Ta có: Nửa chu vi $ \Delta ABC $ : $ p=\dfrac{a+b+c}{2} $ .
Áp dụng công thức Hê-rông: $ S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{12(12-6)(12-8)(12-10)}=24 $
Câu 4: Cho tam giác có ba cạnh lần lượt là $ 3,8,9. $ Góc lớn nhất của tam giác đó có cosin bằng bao nhiêu?
- A
- B
- C
- D
Ta có trong tam giác góc đối diện với cạnh có số đo lớn nhất thì lớn nhất $ \Rightarrow \cos \alpha =\dfrac{{{3}^{2}}+{{8}^{2}}-{{9}^{2}}}{2.3.8}=-\dfrac{1}{6} $
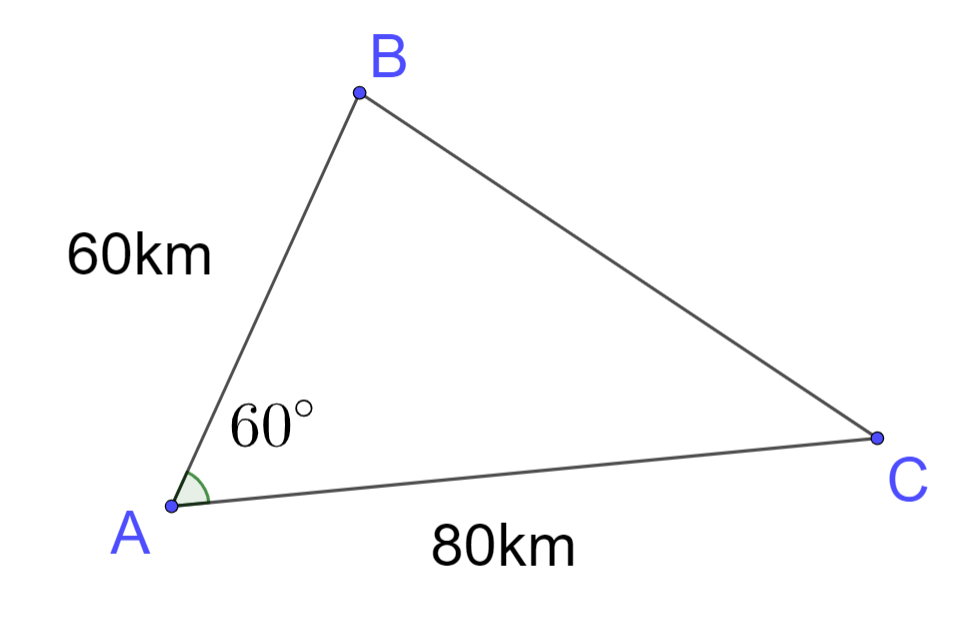
Câu 5: Hai chiếc tàu thủy cũng xuất phát từ vị trí $ A $ , đi thẳng theo hai hướng tạo với nhau một góc $ 60{}^\circ $ . Tàu thứ nhất chạy với tốc độ $ 30km/h $ , tàu thứ hai chạy với tốc độ $ 40km/h $ . Hỏi sau $ 2 $ giờ hai tàu cách nhau bao nhiêu $ km? $
- A
- B
- C
- D

Trong 2 giờ tàu thứ nhất chạy với tốc độ $ 30km/h $ đi được quãng đường $ AB=60\left( km \right) $
Trong 2 giờ tàu thứ nhất chạy với tốc độ $ 40km/h $ đi được quãng đường $ AC=80\left( km \right) $
Xét tam giác $ ABC $ , Độ dài cạnh BC là khoảng cách giữa hai tàu thủy.
$ BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}-2.AB.A\operatorname{C}.\cos 60{}^\circ } $
$ \Leftrightarrow BC=\sqrt{{{60}^{2}}+{{80}^{2}}-2.60.80.\cos 60{}^\circ } $
$ \Leftrightarrow BC=20\sqrt{13}\left( KM \right) $ .
Câu 6: Tam giác $ ABC $ có $ a=6,b=4\sqrt{2},c=2. $ $ M $ là điểm trên cạnh $ BC $ sao cho $ BM=3 $ . Độ dài đoạn $ AM $ bằng bao nhiêu ?
- A
- B
- C
- D
Ta có: Trong tam giác $ ABC $ có $ a=6\Rightarrow BC=6 $ mà $ BM=3 $ suy ra $ M $ là trung điểm $ BC $
Suy ra: $ A{{M}^{2}}=m_{a}^{2}=\dfrac{{{b}^{2}}+{{c}^{2}}}{2}-\dfrac{{{a}^{2}}}{4}=9\Rightarrow AM=3 $
Câu 7: Cho tam giác $ ABC $ , với $m_a$ là đường trung tuyến của tam giác $ABC$ từ đỉnh $A$. $AB=c,AC=b,BC=a$. Chọn công thức đúng trong các đáp án sau?
- A
- B
- C
- D
Ta có: $ m_{a}^{2}=\dfrac{{{b}^{2}}+{{c}^{2}}}{2}-\dfrac{{{a}^{2}}}{4}=\dfrac{2{{b}^{2}}+2{{c}^{2}}-{{a}^{2}}}{4}. $
Câu 8: Độ dài trung tuyến $ {{m}_{c}} $ ứng với cạnh $ c $ của $ \Delta ABC $ bằng biểu thức nào sau đây ?
- A
- B
- C
- D
Ta có: $ m_{c}^{2}=\dfrac{{{b}^{2}}+{{a}^{2}}}{2}-\dfrac{{{c}^{2}}}{4}\Rightarrow {{m}_{c}}=\sqrt{\dfrac{{{b}^{2}}+{{a}^{2}}}{2}-\dfrac{{{c}^{2}}}{4}}=\dfrac{1}{2}\sqrt{(2{{b}^{2}}+2{{a}^{2}})-{{c}^{2}}} $
Câu 9: Cho $ \Delta ABC $ có $AC=6,AB=8,\widehat{A}={{60}^{0}} $ . Độ dài cạnh $BC$ là
- A
- B
- C
- D
Ta có: $ {{BC}^{2}}={{AC}^{2}}+{{AB}^{2}}-2AC.AB\cos A$
\[=36+64-2.6.8.\cos {{60}^{0}}=52\Rightarrow BC=2\sqrt{13} \]