Định luật bảo toàn động lượng
Lý thuyết về Định luật bảo toàn động lượng
+Mối quan hệ giữa động lượng ${{p}_{X}}$ và động năng ${{K}_{X}}$ của hạt X là: $p_{X}^{2}=2{{m}_{X}}{{K}_{X}}$
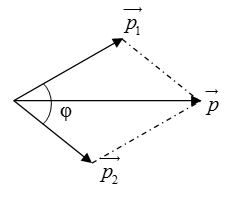
+ Khi tính vận tốc v hay động năng K thường áp dụng quy tắc hình bình hành
Ví dụ: $\overrightarrow{p}=\overrightarrow{{{p}_{1}}}+\overrightarrow{{{p}_{2}}}$ biết $\varphi =\widehat{\overrightarrow{{{p}_{1}}},\overrightarrow{{{p}_{2}}}}$
${{p}^{2}}=p_{1}^{2}+p_{2}^{2}+2{{p}_{1}}{{p}_{2}}cos\varphi $
hay ${{(mv)}^{2}}={{({{m}_{1}}{{v}_{1}})}^{2}}+{{({{m}_{2}}{{v}_{2}})}^{2}}+2{{m}_{1}}{{m}_{2}}{{v}_{1}}{{v}_{2}}cos\varphi $
hay$mK={{m}_{1}}{{K}_{1}}+{{m}_{2}}{{K}_{2}}+2\sqrt{{{m}_{1}}{{m}_{2}}{{K}_{1}}{{K}_{2}}}cos\varphi $
Tương tự khi biết ${{\text{ }\!\!\varphi\!\!\text{ }}_{1}}=\widehat{\overrightarrow{{{p}_{1}}},\overrightarrow{p}}$ hoặc ${{\text{ }\!\!\varphi\!\!\text{ }}_{2}}=\widehat{\overrightarrow{{{p}_{2}}},\overrightarrow{p}}$
Trường hợp đặc biệt:$\overrightarrow{{{p}_{1}}}\bot \overrightarrow{{{p}_{2}}}$ Þ ${{p}^{2}}=p_{1}^{2}+p_{2}^{2}$
Tương tự khi $\overrightarrow{{{p}_{1}}}\bot \overrightarrow{p}$ hoặc $\overrightarrow{{{p}_{2}}}\bot \overrightarrow{p}$
+ $v=0\left( p=0 \right)\Rightarrow {{p}_{1}}={{p}_{2}}$
+ $\dfrac{{{K}_{1}}}{{{K}_{2}}}=\dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{{{m}_{2}}}{{{m}_{1}}}\approx \dfrac{{{A}_{2}}}{{{A}_{1}}}$
Tương tự ${{v}_{1}}=0$ hoặc ${{v}_{2}}=0.$
Bài tập tự luyện có đáp án
Câu 1: Cho phản ứng hạt nhân sau $ _{17}^{37}Cl+X\to n+_{18}^{37}\text{Ar} $ . Hạt nhân X là
- A
- B
- C
- D
Phương trình phản ứng hạt nhân: $ _{17}^{37}Cl+_{1}^{1}X\to n+_{18}^{37}\text{Ar} $
X là $ _{1}^{1}H $.