Độ lệch pha giữa 2 điểm cách nguồn một khoảng x1, x2
Lưu về Facebook:
Lý thuyết về Độ lệch pha giữa 2 điểm cách nguồn một khoảng x1, x2
Xét một sóng hình sin đang lan truyền trong một môi trường theo trục Ox được đặt tại điểm O là:
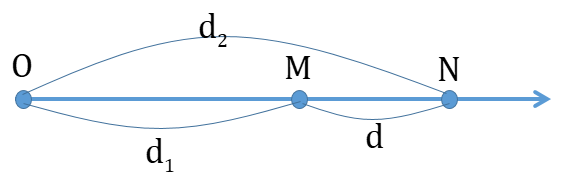
2 điểm M, N cùng phương truyền sóng.
+ M,N cùng phương, cùng phía so với nguồn.
Giả sử:
Độ lệch pha giữa 2 điểm M,N là:
+ M, N cùng phương khác phía so với nguồn.
Giả sử:
Độ lệch pha giữa 2 điểm M,N là:
Bài tập tự luyện có đáp án
Câu 1: Một nguồn sóng (coi như một điểm ) phát sóng cơ trong một môi trường vật chất đẳng hướng , với bước sóng . Hai điểm M,N cùng nằm trên phương truyền sóng cách nguồn sóng các khoảng lần lượt là d1, d2 và cách nhau một khoảng d. Độ lệch pha giữa hai phần tử vật chất tại M, N được tính bởi biểu thức nào sau đây ?
- A
- B
- C
- D

Độ lệch pha giữa hai phần tử vật chất tại M, N:
Câu 2: Hai sóng dao động cùng pha khi độ lệch pha của hai sóng bằng
- A
- B
- C
- D
Hai dao động cùng pha khi:
Xem thêm các bài tiếp theo bên dưới