Biên độ dao động tổng hợp
Lý thuyết về Biên độ dao động tổng hợp
${x_1} ;{x_2}$ là phương trình dao động thành phần và x là phương trình dao động tổng hợp.
$\left. \begin{align}& {{x}_{1}}={{A}_{1}}\cos \left( \omega t+{{\varphi }_{1}} \right) \\ & {{x}_{2}}={{A}_{2}}\cos \left( \omega t+{{\varphi }_{2}} \right) \\ \end{align} \right\}\Rightarrow x=A\cos \left( \omega t+\varphi \right)$
${{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}c\text{os}({{\varphi }_{2}}-{{\varphi }_{1}})$
Bài tập tự luyện có đáp án
Câu 1: Hai dao động điều hoà cùng phương, biên độ a bằng nhau, chu kì T bằng nhau và có hiệu pha ban đầu \(\Delta \varphi \) = 2\(\pi \)/3. Dao động tổng hợp của hai dao động đó sẽ có biên độ bằng
- A
- B
- C
- D
\({{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos (\dfrac{2\pi }{3})={{A}^{2}}\)
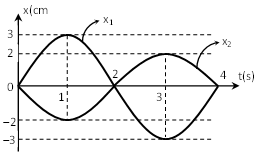
Câu 2:  Đồ thị của hai dao động điều hòa cùng tần số được vẽ như sau: Phương trình nào sau đây là phương trình dao động tổng hợp của chúng:
Đồ thị của hai dao động điều hòa cùng tần số được vẽ như sau: Phương trình nào sau đây là phương trình dao động tổng hợp của chúng:
 Đồ thị của hai dao động điều hòa cùng tần số được vẽ như sau: Phương trình nào sau đây là phương trình dao động tổng hợp của chúng:
Đồ thị của hai dao động điều hòa cùng tần số được vẽ như sau: Phương trình nào sau đây là phương trình dao động tổng hợp của chúng:- A
- B
- C
- D
Từ đồ thị ta có : \(T=4\text{ }s~\Rightarrow ~\omega =\text{ }\dfrac{2\pi }{4}=~\dfrac{\pi }{2}\)
\({{A}_{1}}~=\text{ }3\text{ }cm~\Rightarrow \text{ }{{x}_{1}}=\text{ }3cos\left( \dfrac{\pi }{2}t\text{ }\dfrac{\pi }{2}~ \right)\)
\({{A}_{2}}~=\text{ }2cm~\Rightarrow ~~~{{x}_{2}}=\text{ }2cos\left( \dfrac{\pi }{2}t\text{ }+\dfrac{\pi }{2}~ \right)\)
Hai dao động ngược pha : \(A\text{ }=\text{ }{{A}_{1}}~\text{ }{{A}_{2}}~=\text{ }1\text{ }cm\)
Do \({{A}_{1}}~>\text{ }{{A}_{2}}~\) nên \(\varphi ~=~{{\varphi }_{1}}~=\text{ }-~\dfrac{\pi }{2}\)
Câu 3: Chọn câu đúng. Nếu hai dao động điều hoà cùng tần số, cùng pha thì li độ của chúng:
- A
- B
- C
- D
Xét hai dao động cùng pha.
$x_1 = A_1.cos(ωt + φ)$ và $x_2 = A_2.cos(ωt + φ)$.
rõ ràng khi $A_1 = A_2$ thì $x_1 = x_2$.
Câu 4: Chọn câu đúng. Một vật thực hiện đồng thời hai dao động điều hoà có phương trình dao động $x_1 = A_1.cos(ωt + φ_1)$ và $x_2 = A_2.cos(ωt + φ_2)$. Biên độ của dao động tổng hợp được xác định là
- A
- B
- C
- D
Dùng giản đồ vecto để tổng hợp hai dao động điều hòa cùng phương, cùng tần số.
$\overrightarrow A = \overrightarrow {{A_1}} + \overrightarrow {{A_2}} $
Dễ thấy
$A^2= A_1^2+ A_2^2+ 2A_1 A_2 c{\rm{os(}}\varphi _{\rm{1}}- \varphi _2 )$

Xem thêm các bài tiếp theo bên dưới