Định nghĩa, tính chất, biểu thức tọa độ của phép đối xứng trục
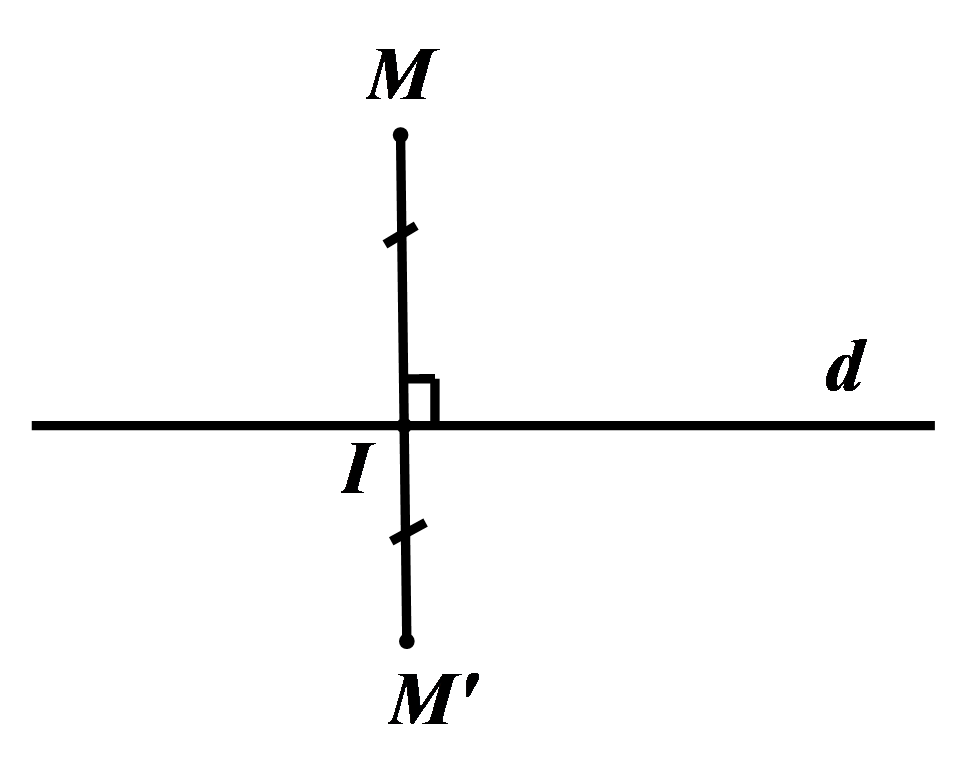
Lý thuyết về Định nghĩa, tính chất, biểu thức tọa độ của phép đối xứng trục
1. Định nghĩa
Cho đường thẳng \[d\]. Phép biến hình biến mỗi điểm \[M\] thuộc \[d\] thành chính nó, biến mỗi điểm \[M\] không thuộc \[d\] thành điểm \[M'\] sao cho \[d\] là đường trung trực của đoạn \[MM'\] được gọi là phép đối xứng qua đường thẳng \[d\], hay còn gọi là phép đối xứng trục \[d\].
Phép đối xứng trục có trục là đường thẳng \[d\] được kí hiệu là \[{{Đ}_{d}}\]. Như vậy \[{{Đ}_{d}}\left( M \right)=M'\Leftrightarrow \overrightarrow{IM}=-\overrightarrow{IM'}\] với \[I\] là hình chiếu vuông góc của \[M\] trên \[d\].
Nếu \[{{Đ}_{d}}\left[ \left( H \right) \right]=\left( H \right)\] thì \[d\] được gọi là trục đối xứng của hình \[\left( H \right)\].
2. Biểu thức tọa độ của phép đối xứng trục
Trong mặt phẳng \[Oxy\], với mỗi điểm \[M\left( x;y \right)\], gọi \[M'\left( x';y' \right)={{Đ}_{d}}\left( M \right)\].
Nếu chọn \[d\] là trục \[Ox\], thì \[\left\{ \begin{array}{l}
x' = x\\
y' = - y
\end{array} \right.\]
Nếu chọn \[d\] là trục \[Oy\], thì \[\left\{ \begin{array}{l}
x' = - x\\
y' = y
\end{array} \right.\]
3. Tính chất phép đối xứng trục
- Bảo toàn khoảng cách giữa hai điểm bất kì.
- Biến một đường thẳng thành đường thẳng.
- Biến một đoạn thẳng thành đoạn thẳng bằng đoạn đã cho.
- Biến một tam giác thành tam giác bằng tam giác đã cho.
- Biến đường tròn thành đường tròn có cùng bán kính.
Bài tập tự luyện có đáp án
Câu 1: Qua phép đối xứng trục $Oy$ biến điểm \(M\left( x;y \right)\) thành \(M'\left( x';y' \right)\) thì:
- A
- B
- C
- D
Cách 2: Áp dụng biểu thức giải tích của phép đối xứng trục với \({Oy}:x=0\)
Câu 2: Giả sử ${{D}_{a}}(M)=M',\left( M\ne M' \right)$. Mệnh đề nào sau đây là sai?
- A
- B
- C
- D
Dựa vào lý thuyết phép đối xứng trục.
Câu 3: Qua phép đối xứng trục $Ox$ biến điểm \(M\left( x;y \right)\) thành \(M'\left( x';y' \right)\) thì
- A
- B
- C
- D
Cách 2: Áp dụng biểu thức giải tích của phép đối xứng trục với \({Ox}:y=0\)
Câu 4:
Trong các mệnh đề sau, mệnh đề nào đúng?
Trong các mệnh đề sau, mệnh đề nào đúng?
- A
- B
- C
- D
Câu 5: Hình nào dưới đây không có trục đối xứng?
- A
- B
- C
- D
Câu 6: Cho $A\left( 1;2 \right)$, ảnh của $A$ qua phép đối xứng trục \(Ox\) là:
- A
- B
- C
- D
& x'=x \\
& y'=-y \\
\end{align} \right.$ nên ảnh của $A$ qua phép đối xứng trục \(Ox\) là $\left( 1;-2 \right)$
Câu 7:
Trong mặt phẳng tọa độ \(\text{Oxy}\) , cho phép biến hình $ F: M\left( x;y \right)\to M'\left( y;x \right) $ . Chọn mệnh đề đúng.
Trong mặt phẳng tọa độ \(\text{Oxy}\) , cho phép biến hình $ F: M\left( x;y \right)\to M'\left( y;x \right) $ . Chọn mệnh đề đúng.
- A
- B
- C
- D
Câu 8:
Cho hai đường thẳng cắt nhau $ d $ và $ d' $ . Có bao nhiêu phép đối xứng trục biến đường thẳng này thành đường thẳng kia?
Cho hai đường thẳng cắt nhau $ d $ và $ d' $ . Có bao nhiêu phép đối xứng trục biến đường thẳng này thành đường thẳng kia?
- A
- B
- C
- D
Câu 9: Hình nào trong các hình sau có duy nhất một trục đối xứng:
- A
- B
- C
- D
Hình thang và hình bình hành(không phải các trường hợp đặc biệt) không có trục đối xứng
Tam giác đều có ba trục đối xứng là ba đường cao kẻ từ ba đỉnh
Tam giác cân chỉ có 1 trục đối xứng
Câu 10:
Cho đường thẳng $ a $ . Qua phép đối xứng trục $ a $ , đường thẳng nào biến thành chính nó.
Cho đường thẳng $ a $ . Qua phép đối xứng trục $ a $ , đường thẳng nào biến thành chính nó.
- A
- B
- C
- D
Lấy $ A\in l $ và $ {{D}_{a}}\left( A \right)=A'\Rightarrow AA'\bot a\Rightarrow A'\in l $ và ngược lại vẫn thỏa mãn \(\Rightarrow {{D}_{a}}\left( l \right)=l\).
Câu 11: Giả sử ${{D}_{a}}(A)=A',\ {{D}_{a}}(B)=B'$. Mệnh đề nào sau đây đúng?
- A
- B
- C
- D