Phương trình chính tắc elip

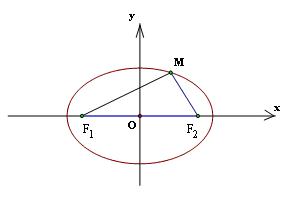
Cho elip $(E)$ như trong định nghĩa. Ta chọn hệ trục tọa độ $Oxy$ có gốc là trung điểm đoạn thẳng $F1F2$. Trục $Oy$ là trung trực của $F1F2$ và $F2$ nằm trên tia $Ox$
  
Các đoạn thẳng $MF1,MF2$ được gọi là bán kính qua tiêu của điểm $M$. Bây giờ ta lập phương trình của elip $(E)$ đối với hệ trục tọa độ đã chọn như trên.
Ta có:
$M{{F}_{1}}=a+\dfrac{cx}{a}=\sqrt[{}]{{{\left( x+c \right)}^{2}}+{{y}^{2}}}$ hay${{\left( a+\dfrac{cx}{a} \right)}^{2}}={{\left( x+c \right)}^{2}}+{{y}^{2}}$
Rút gọn đẳng thức trên ta được$\left( 1-\dfrac{{{c}^{2}}}{{{a}^{2}}} \right){{x}^{2}}+{{y}^{2}}={{a}^{2}}-{{c}^{2}}$, hay $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{a}^{2}}-{{c}^{2}}}=1$ vì ${{a}^{2}}-{{c}^{2}}>0$ nên ta có thể đặt ${{a}^{2}}-{{c}^{2}}={{b}^{2}}$ (với b > 0) và được 
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ $(a>b>0)$               (1)
Phương trình (1) gọi là phương trình chính tắc của elip đã cho.
Ví dụ : Viết phương trình chính tắc của elip đi qua hai điểm M(0;1) và 
$N\left( 1;\dfrac{\sqrt[{}]{3}}{2} \right)$ . Xác định toạ độ các tiêu điểm của elip đó 
Giải : Phương trình chính tắc của elip có dạng $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ $(a>b>0)$                                           

Elip đi qua $M ( 0;1)$ nên $\dfrac{1}{{{b}^{2}}}=1$hay${{b}^{2}}=1$. Elip đó đi qua$N\left( 1;\dfrac{\sqrt[{}]{3}}{2} \right)$nên $\dfrac{1}{{{a}^{2}}}+\dfrac{3}{4{{b}^{2}}}=1$
Suy ra ${{a}^{2}}=4$. Vậy elip cần tìm cho phương trình chính là $\dfrac{{{x}^{2}}}{4}+\dfrac{{{y}^{2}}}{1}=1$
Ta có ${{c}^{2}}={{a}^{2}}-{{b}^{2}}=4-1=3$. Vậy toạ độ các tiêu điểm của elip đó là 
$F1\left( -\sqrt[{}]{3};0 \right)$ và $F2\left( \sqrt[{}]{3};0 \right)$