Mạch điện xoay chiều chỉ chứa một phần tử

1. Mạch xoay chiều chỉ chứa R

Điện trở thuần biến toàn bộ điện năng qua nó thành nhiệt.

Đặt vào 2 đầu 1 điện áp xoay chiều: $u={{U}_{0}}cos(\omega t+\varphi )$

Xét $\Delta t$ vô cùng nhỏ thì dòng xoay chiều như dòng 1 chiều. Theo định luật Ôm.

$i=\dfrac{u}{R}\Rightarrow i=\dfrac{{{U}_{0}}}{R}\cos \left( \omega t+\varphi  \right)={{I}_{0}}\cos \left( \omega t+\varphi  \right)$ với ${{I}_{0}}=\dfrac{{{U}_{0}}}{R}$

Trong mạch chỉ chứa R: u và i cùng pha.

Chú ý: công thức tính điện trở dây dẫn: $R=\rho \dfrac{\ell }{S}$

Trong đó: 

R là điện trở dây dẫn $\left( \Omega  \right)$

$\rho $ là điện trở suất của dây dẫn $\left( \Omega .m \right)$

$\ell $ là chiều dài dây dẫn (m)

S là tiết diện của dây dẫn $\left( {{m}^{2}} \right)$

2. Mạch điện xoay chiều chỉ chứa cuộn cảm

Cuộn thuần cảm là cuộn cảm lí tưởng không có điện trở thuần ( đặc trưng cho cuộn thuần cảm là độ tự cảm L)

Dòng 1 chiều đi qua được cuộn thuần cảm ( lúc này cuộn như dây dẫn không có điện trở R)

Dòng xoay chiều cũng đi qua cuộn thuần cảm nhưng bị cản trở 1 phần. Đại lượng vật lí đặc trưng cho sự cản trở dòng điện của cuộn cảm là cảm kháng:

${{Z}_{L}}=\omega L\left( \Omega  \right)$ $\Rightarrow I=\dfrac{U}{{{Z}_{L}}}$; ${{I}_{0}}=\dfrac{{{U}_{0}}}{{{Z}_{L}}}$

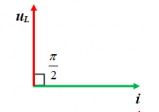
${{u}_{L}}$ nhanh pha hơn i là $\pi /2$ ,$(\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}=\pi /2)$

Ta luôn có: $\dfrac{{{u}^{2}}}{{{U}^{2}}}\ +\ \dfrac{{{i}^{2}}}{{{I}^{2}}}\ =\ 2.$ ; $\dfrac{{{u}^{2}}}{U_{0}^{2}}+\dfrac{{{i}^{2}}}{I_{0}^{2}}=1$

3. Mạch điện xoay chiều chỉ chứa tụ điện

Tụ điện không cho dòng 1 chiều đi qua.

Tụ điện cho dòng xoay chiều đi qua nhưng cản trở 1 phần. Đại lượng vật lí đặc trưng cho sự cản trở này được gọi là dung kháng

${{Z}_{C}}=\dfrac{1}{\omega C}$ Trong đó C là điện dung của tụ điện (F)

$\Rightarrow I=\dfrac{U}{{{Z}_{C}}}$; ${{I}_{0}}=\dfrac{{{U}_{0}}}{{{Z}_{C}}}$

${{u}_{L}}$ nhanh pha hơn i là$\pi /2$ ,$(\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}=\pi /2)$

Ta luôn có: $\dfrac{{{u}^{2}}}{{{U}^{2}}}\ +\ \dfrac{{{i}^{2}}}{{{I}^{2}}}\ =\ 2.$ ; $\dfrac{{{u}^{2}}}{U_{0}^{2}}+\dfrac{{{i}^{2}}}{I_{0}^{2}}=1$