Mặt cầu ngoại tiếp khối chóp, lăng trụ
Lý thuyết về Mặt cầu ngoại tiếp khối chóp, lăng trụ
1. Chóp có các đỉnh cùng nhìn đoạn thẳng nối hai đỉnh còn lại dưới 1 góc vuông:
Gọi độ dài đoạn thẳng nối hai đỉnh đó là dd.
Khi đó bán kính mặt cầu ngoại tiếp chóp được tính bằng công thức: R=d2R=d2 .
2. Chóp có cạnh bên vuông góc với đáy:
Chóp đa giác có cạnh bên SASAvuông góc với đáy. Gọi RdRd là bán kính đường tròn ngoại tiếp đáy.
Khi đó bán kính mặt cầu ngoại tiếp chóp được tính bằng công thức: R=√SA24+R2dR=√SA24+R2d .
3. Chóp có mặt bên vuông góc với đáy:
Chóp đa giác có mặt bên (SAB)(SAB)vuông góc với đáy. Gọi RdRd là bán kính đường tròn ngoại tiếp đáy, RbRb là bán kính đường tròn ngoại tiếp mặt bên(SAB)(SAB).
Khi đó bán kính mặt cầu ngoại tiếp chóp được tính bằng công thức: R=√R2d+R2b−AB24R=√R2d+R2b−AB24.
4. Chóp đều:
Chóp đều có cạnh bên SASA, chiều cao là SOSOvà RdRd là bán kính đường tròn ngoại tiếp đáy.
Khi đó bán kính mặt cầu ngoại tiếp chóp được tính bằng công thức: R=SA22SO=SA22√SA2−R2dR=SA22SO=SA22√SA2−R2d.
Lăng trụ đứng có cạnh bên AA′, bán kính đường tròn ngoại tiếp đáy là Rd.
Khi đó bán kính mặt cầu ngoại tiếp lăng trụ này được tính bằng công thức:R=√AA′24+R2d.
Bài tập tự luyện có đáp án
Câu 1: Trong các đa diện sau, đa diện không nội tiếp mặt cầu là
- A
- B
- C
- D
Do không phải tứ giác nào cũng có đường tròn ngoại tiếp nên tồn tại chóp có đáy là tứ giác không nội tiếp mặt cầu.
Câu 2: Cho khối cầu có thể tích bằng 36π . Bán kính của khối cầu đã cho bằng
- A
- B
- C
- D
Ta có V=43πR3⇔36π=43πR3⇔R3=27⇔R=3 .
Vậy bán kính của khối cầu đã cho bằng 3 .
Câu 3: Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông cân tại A, AB=AC=a, AA ′ =√2a. Thể tích khối cầu ngoại tiếp hình tứ diện AA′B′C′ là
- A
- B
- C
- D
Bán kính đáy đường tròn ngoại tiếp đáy r=BC2=a√22
Áp dụng công thức tính nhanh ta có: R=√r2+(AA′2)2=a⇒V=43πR3=43πa3
Câu 4: Một khối cầu tiếp xúc với tất cả các mặt của hình lập phương. Tỉ số thể tích giữa khối cầu và khối lập phương đó bằng:
Một khối cầu tiếp xúc với tất cả các mặt của hình lập phương. Tỉ số thể tích giữa khối cầu và khối lập phương đó bằng:
- A
- B
- C
- D
Giả sử cạnh của hình lập phương a, khi đó bán kính khối cầu là a2
Thể tích của khối cầu là V1=43π(a2)3=πa36
Thể tích hình lập phương V2=a3. Ta có V1V2=π6.
Câu 5: Cho hình lập phương ABCD.A′B′C′D′ . Chọn khẳng định đúng trong các khẳng định sau?
- A
- B
- C
- D

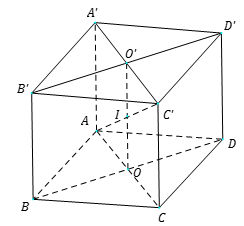
Giả sử ta có hình lập phương như hình vẽ.
Ta thấy khoảng cách từ trung điểm I của AC′ đến các mặt phẳng bằng nhau nên tâm mặt cầu nội tiếp hình lập phương là trung điểm cạnh AC′
Câu 6: Cho các hình chóp lần lượt có đáy là: tam giác, hình bình hành, hình thoi, hình vuông, hình chữ nhật. Số hình chóp không có mặt cầu ngoại tiếp là
- A
- B
- C
- D
Như ta đã biết thì hình chóp mà có đáy nội tiếp hình tròn thì hình chóp đó có mặt cầu ngoại tiếp. Trong các đáy trên có hình bình hành và hình thoi là không có đường tròn ngoại tiếp nên suy ra đáp án cần chọn là 2.