Xác định dấu của nghiệm phương trình bậc 2
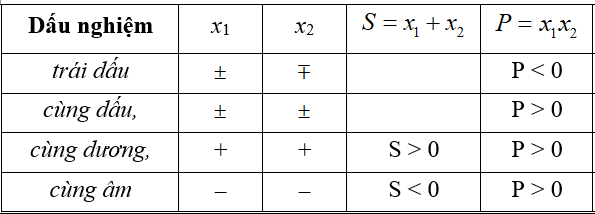
Lý thuyết về Xác định dấu của nghiệm phương trình bậc 2
Cho phương trình: $a{x^2} + bx + c = 0\left( {a \ne 0} \right)$ . Điều kiện để phương trình có 2 nghiệm: trái dấu, cùng dấu, cùng dương, cùng âm ….
Bài tập tự luyện có đáp án
Câu 1: Cho phương trình $ {{x}^{2}}-3x-7=0 $ có 2 nghiệm $ {{x}_{1}} $ và $ {{x}_{2}} $ . Tính $ x_{1}^{2}+x_{2}^{2} $ .
- A
- B
- C
- D
Phương trình có $ \Delta ={{3}^{2}}+4.7=37 > 0 $ .
Theo hệ thức Vi-ét ta có: $ \left\{ \begin{array}{l} & {{x}_{1}}+{{x}_{2}}=3 \\ & {{x}_{1}}{{x}_{2}}=-7 \end{array} \right. $ .
Khi đó $ x_{1}^{2}+x_{2}^{2}={{({{x}_{1}}+{{x}_{2}})}^{2}}-2{{x}_{1}}{{x}_{2}}={{3}^{2}}-2.(-7)=23. $
Câu 2: Cho phương trình $ {{x}^{2}}-5x-1=0 $ có 2 nghiệm $ {{x}_{1}} $ và $ {{x}_{2}} $ . Giá trị của biểu $ x_{1}^{4}+x_{2}^{4} $ là
- A
- B
- C
- D
Phương trình có $ \Delta ={{5}^{2}}+4=29 > 0. $
Hệ thức Vi-ét: $ \left\{ \begin{array}{l} & {{x}_{1}}+{{x}_{2}}=5 \\ & {{x}_{1}}{{x}_{2}}=-1 \end{array} \right.. $
Khi đó:
$ \begin{array}{l} & x_{1}^{4}+x_{2}^{4}={{\left( x_{1}^{2}+x_{2}^{2} \right)}^{2}}-2x_{1}^{2}x_{2}^{2}={{\left[ {{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-2{{x}_{1}}{{x}_{2}} \right]}^{2}}-2x_{1}^{2}x_{2}^{2} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,={{\left[ {{5}^{2}}-2.(-1) \right]}^{2}}-2{{(-1)}^{2}}=727 \end{array} $
Câu 3: Cho phương trình: $ {{x}^{2}}-3x-1=0 $ có 2 nghiệm $ {{x}_{1}} $ và $ {{x}_{2}} $ . Tính giá trị của biểu thức $ P=\dfrac{{{x}_{1}}}{{{x}_{2}}+1}+\dfrac{{{x}_{2}}}{{{x}_{1}}+1} $ .
- A
- B
- C
- D
Phương trình có $ \Delta ={{3}^{2}}+4=13 > 0 $
Hệ thức Vi-ét $ \left\{ \begin{array}{l} & {{x}_{1}}+{{x}_{2}}=3 \\ & {{x}_{1}}{{x}_{2}}=-1 \end{array} \right.. $
$ \begin{array}{l} & P=\dfrac{{{x}_{1}}}{{{x}_{2}}+1}+\dfrac{{{x}_{2}}}{{{x}_{1}}+1}=\dfrac{x_{1}^{2}+x_{2}^{2}+\left( {{x}_{1}}+{{x}_{2}} \right)}{\left( {{x}_{1}}+1 \right)\left( {{x}_{2}}+1 \right)} \\ & =\dfrac{{{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}+\left( {{x}_{1}}+{{x}_{2}} \right)-2{{x}_{1}}{{x}_{2}}}{{{x}_{1}}{{x}_{2}}+{{x}_{1}}+{{x}_{2}}+1} \\ & =\dfrac{{{3}^{2}}+3-2.(-1)}{(-1)+3+1}=\dfrac{14}{3}. \end{array} $
Câu 4: Cho phương trình $ 3x(x-2)+(x-1)(x-3)+2=0 $ có 2 nghiệm $ {{x}_{1}} $ và $ {{x}_{2}} $ . Tính $ x_{1}^{3}+x_{2}^{3} $ .
- A
- B
- C
- D
$ \begin{array}{l} & 3x(x-2)+(x-1)(x-3)+2=0 \\ & \Leftrightarrow 3{{x}^{2}}-6x+{{x}^{2}}-4x+3+2=0 \\ & \Leftrightarrow 4{{x}^{2}}-10x+5=0. \end{array} $
Phương trình có $ \Delta '={{5}^{2}}-4.5=5 > 0 $.
Theo hệ thức Vi-ét ta có $ \left\{ \begin{array}{l} & {{x}_{1}}+{{x}_{2}}=\dfrac{5}{2} \\ & {{x}_{1}}{{x}_{2}}=\dfrac{5}{4} \end{array} \right.. $
Khi đó $ x_{1}^{3}+x_{2}^{3}={{\left( {{x}_{1}}+{{x}_{2}} \right)}^{3}}-3{{x}_{1}}{{x}_{2}}\left( {{x}_{1}}+{{x}_{2}} \right)={{\left( \dfrac{5}{2} \right)}^{3}}-3.\dfrac{5}{4}.\dfrac{5}{2}=\dfrac{25}{4}. $
Câu 5: Cho phương trình: $ \sqrt{2}{{x}^{2}}-4x+1=0 $ có 2 nghiệm $ {{x}_{1}} $ và $ {{x}_{2}} $ . Tính giá trị của biểu thức $ B=x_{1}^{2}+x_{2}^{2}-{{x}_{1}}{{x}_{2}} $
- A
- B
- C
- D
Phương trình có $ \Delta '={{2}^{2}}-\sqrt{2}=4-\sqrt{2}\,\, > 0 $
Hệ thức Vi-ét $ \left\{ \begin{array}{l} & {{x}_{1}}+{{x}_{2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2} \\ & {{x}_{1}}{{x}_{2}}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2} \end{array} \right.. $
Khi đó: $ B=x_{1}^{2}+x_{2}^{2}-{{x}_{1}}{{x}_{2}}={{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-3{{x}_{1}}{{x}_{2}}={{\left( 2\sqrt{2} \right)}^{2}}-3.\dfrac{\sqrt{2}}{2}=\dfrac{16-3\sqrt{2}}{2}. $
Câu 6: Cho phương trình $ {{x}^{2}}-\sqrt{3}x-2=0 $ có $2$ nghiệm $ {{x}_{1}} $ và $ {{x}_{2}} $ . Giá trị của biểu thức $ \dfrac{{{x}_{1}}}{{{x}_{2}}}+\dfrac{{{x}_{2}}}{{{x}_{1}}} $ là
- A
- B
- C
- D
Phương trình có: $ \Delta ={{\left( \sqrt{3} \right)}^{2}}-4.(-2)=11 > 0 $
Ta có hệ thức Vi-ét: $ \left\{ \begin{array}{l} & {{x}_{1}}+{{x}_{2}}=\sqrt{3} \\ & {{x}_{1}}{{x}_{2}}=-2 \end{array} \right. $
Khi đó: $ \dfrac{{{x}_{1}}}{{{x}_{2}}}+\dfrac{{{x}_{2}}}{{{x}_{1}}}=\dfrac{x_{1}^{2}+x_{2}^{2}}{{{x}_{1}}{{x}_{2}}}=\dfrac{{{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-2{{x}_{1}}{{x}_{2}}}{{{x}_{1}}{{x}_{2}}}=\dfrac{3-2(-2)}{-2}=-\dfrac{7}{2}. $
Câu 7: Cho phương trình: $ 3{{x}^{2}}-6x+2=0 $ có 2 nghiệm $ {{x}_{1}} $ và $ {{x}_{2}} $ . Tính giá trị của biểu thức: $ A=\dfrac{1-{{x}_{1}}}{{{x}_{1}}}+\dfrac{1-{{x}_{2}}}{{{x}_{2}}} $ .
- A
- B
- C
- D
Phương trình có $ \Delta '={{(-3)}^{2}}-3.2=3 > 0 $
Ta có hệ thức Vi-ét $ \left\{ \begin{array}{l} & {{x}_{1}}+{{x}_{2}}=2 \\ & {{x}_{1}}{{x}_{2}}=\dfrac{2}{3} \end{array} \right.. $
Khi đó: $ A=\dfrac{1-{{x}_{1}}}{{{x}_{1}}}+\dfrac{1-{{x}_{2}}}{{{x}_{2}}}=\dfrac{{{x}_{1}}+{{x}_{2}}-2{{x}_{1}}{{x}_{2}}}{{{x}_{1}}{{x}_{2}}}=\dfrac{2-2.\dfrac{2}{3}}{\dfrac{2}{3}}=1. $
Câu 8: Cho phương trình: $ x\left( 2x-1 \right)+3x-2=0 $ có 2 nghiệm $ {{x}_{1}} $ và $ {{x}_{2}} $ . Tính giá trị của biểu thức: $ P=\dfrac{x_{1}^{2}+4{{x}_{1}}{{x}_{2}}+x_{2}^{2}}{3{{x}_{1}}x_{2}^{2}+3x_{1}^{2}{{x}_{2}}}. $
- A
- B
- C
- D
$ x\left( 2x-1 \right)+3x-2=0\Leftrightarrow {{x}^{2}}+x-1=0. $
Phương trình có $ \Delta ={{1}^{2}}-4.1.(-1)=5\, > 0 $
Hệ thức Vi-ét $ \left\{ \begin{array}{l} & {{x}_{1}}+{{x}_{2}}=-1 \\ & {{x}_{1}}{{x}_{2}}=-1 \end{array} \right. $ .
Khi đó: $ P=\dfrac{x_{1}^{2}+4{{x}_{1}}{{x}_{2}}+x_{2}^{2}}{3{{x}_{1}}x_{2}^{2}+3x_{1}^{2}{{x}_{2}}}=\dfrac{{{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}+2{{x}_{1}}{{x}_{2}}}{3{{x}_{1}}{{x}_{2}}\left( {{x}_{1}}+{{x}_{2}} \right)}=\dfrac{{{(-1)}^{2}}+2(-1)}{3.(-1).(-1)}=-\dfrac{1}{3}. $
Câu 9: Cho phương trình: $ \left( {{x}^{2}}+4x \right)\left( {{x}^{2}}+4x+5 \right)-14=0 $ . Tính tích các nghiệm của phương trình.
- A
- B
- C
- D
Đặt $ t={{x}^{2}}+4x $ ta có phương trình
$ t(t+5)-14=0\Leftrightarrow {{t}^{2}}+5t-14=0\,\,\,\Leftrightarrow \left[ \begin{array}{l} & t=-7 \\ & t=2 \end{array} \right.. $
Với $ t=-7\,\,\Rightarrow \,{{x}^{2}}+4x=-7\Leftrightarrow {{x}^{2}}+4x+7=0 $ (phương trình vô nghiệm)
Với $ t=2 $ $ \Rightarrow \,{{x}^{2}}+4x=2\Leftrightarrow {{x}^{2}}+4x-2=0\,\,\,(1) $
Phương trình (1) có $ ac=-2 < 0 $
$ \Rightarrow $ (1) có 2 nghiệm trái dấu $ {{x}_{1}} $ và $ {{x}_{2}} $
Theo hệ thức Vi-ét ta có: $ {{x}_{1}}.{{x}_{2}}=-2. $
Câu 10: Cho phương trình $ 2\left( {{x}^{2}}-1 \right)+3x-5=0 $ có 2 nghiệm $ {{x}_{1}} $ và $ {{x}_{2}} $ . Tính giá trị của biểu thức $ P={{x}_{1}}x_{2}^{2}+x_{1}^{2}{{x}_{2}} $ .
- A
- B
- C
- D
$ \begin{array}{l} & 2\left( {{x}^{2}}-1 \right)+3x-5=0 \\ & \Leftrightarrow 2{{x}^{2}}+3x-7=0 \end{array} $
Phương trình có $ \Delta ={{3}^{2}}-4.2(-7)=65 > 0 $.
Theo hệ thức Vi-ét ta có: $ \left\{ \begin{array}{l} & {{x}_{1}}+{{x}_{2}}=-\dfrac{3}{2} \\ & {{x}_{1}}{{x}_{2}}=-\dfrac{7}{2} \end{array} \right. $.
Khi đó $ P={{x}_{1}}x_{2}^{2}+x_{1}^{2}{{x}_{2}}={{x}_{1}}{{x}_{2}}\left( {{x}_{1}}+{{x}_{2}} \right)=\left( -\dfrac{7}{2} \right).\left( -\dfrac{3}{2} \right)=\dfrac{21}{4} $ .
Câu 11: Phương trình $ {{x}^{3}}-15x+22=0 $ có 1 nghiệm $ x=2 $ . Tính tổng các nghiệm còn lại của phương trình.
- A
- B
- C
- D
$ \begin{array}{l} & {{x}^{3}}-15x+22=0 \\ & \Leftrightarrow (x-2)\left( {{x}^{2}}+2x-11 \right)=0 \\ & \Leftrightarrow \left[ \begin{array}{l} & x=2 \\ & {{x}^{2}}+2x-11=0\,\,\,(1) \end{array} \right. \end{array} $
Phương trình (1) luôn có 2 nghiệm $x_1;x_2$
Theo hệ thức Vi-ét ta có: $ {{x}_{1}}+{{x}_{2}}=-2. $
Câu 12: Cho phương trình: $ {{x}^{2}}-(m+2)x+2m=0 $ ( $ m $ là tham số) có 2 nghiệm $ {{x}_{1}} $ và $ {{x}_{2}} $ . Tính theo $ m $ giá trị của biểu thức $ P={{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}} $ .
- A
- B
- C
- D
Phương trình có $ \Delta ={{(m+2)}^{2}}-8m={{m}^{2}}-4m+4={{(m-2)}^{2}}\ge 0 $
Hệ thức Vi-ét: $ \left\{ \begin{array}{l} & {{x}_{1}}+{{x}_{2}}=m+2 \\ & {{x}_{1}}{{x}_{2}}=2m \end{array} \right.. $
$ P={{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}={{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-4{{x}_{1}}{{x}_{2}}={{(m+2)}^{2}}-4.2m={{\left( m-2 \right)}^{2}} $
Câu 13: Cho phương trình: $ {{x}^{4}}-3{{x}^{3}}+2{{x}^{2}}-3x+1=0 $ có 2 nghiệm $ {{x}_{1}} $ và $ {{x}_{2}} $ . Tính giá trị của biểu thức: $ A={{x}_{1}}+{{x}_{2}}-{{x}_{1}}{{x}_{2}} $ .
- A
- B
- C
- D
$ \begin{array}{l} & {{x}^{4}}-3{{x}^{3}}+2{{x}^{2}}-3x+1=0 \\ & \Leftrightarrow \left( {{x}^{4}}+{{x}^{2}} \right)-\left( 3{{x}^{3}}+3x \right)+\left( {{x}^{2}}+1 \right)=0 \\ & \Leftrightarrow {{x}^{2}}\left( {{x}^{2}}+1 \right)-3x\left( {{x}^{2}}+1 \right)+\left( {{x}^{2}}+1 \right)=0 \\ & \Leftrightarrow \left( {{x}^{2}}+1 \right)\left( {{x}^{2}}-3x+1 \right)=0 \\ & \Leftrightarrow {{x}^{2}}-3x+1=0\,\,\,(1) \end{array} $
Phương trình (1) có $ \Delta ={{3}^{2}}-4=5\, > 0 $
Hệ thức Vi-ét $ \left\{ \begin{array}{l} & {{x}_{1}}+{{x}_{2}}=3 \\ & {{x}_{1}}{{x}_{2}}=1 \end{array} \right.. $
Khi đó: $ A={{x}_{1}}+{{x}_{2}}-{{x}_{1}}{{x}_{2}}=3-1=2. $
Xem thêm các bài tiếp theo bên dưới