Hệ hai phương trình bậc nhất hai ẩn
Lý thuyết về Hệ hai phương trình bậc nhất hai ẩn
Mỗi cặp số (x0;y0) thỏa mãn (I) được gọi là một nghiệm của hệ.
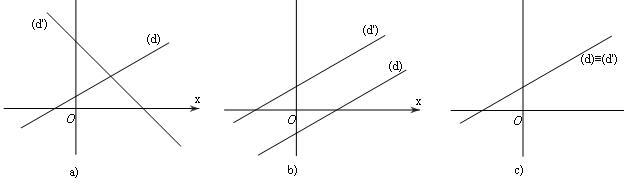
Giả sử (d) là đường thẳng ax+by=c và (d′) là đường thẳng a′x+b′y=c′. Khi đó:
1) Hệ (I) có nghiệm duy nhất ⇔ (d) và (d′) cắt nhau;
2) Hệ (I) vô nghiệm⇔ (d) và (d′) song song với nhau;
3) Hệ (I) có vô số nghiệm ⇔ (d) và (d′) trùng nhau.
Bài tập tự luyện có đáp án
Câu 1: Hệ phương trình {|x|−3√2y=122|x|−√2y=4 có bao nhiêu nghiệm?
- A
- B
- C
- D
{|x|−3√2y=122|x|−√2y=4⇔{|x|−3√2y=126|x|−3√2y=12⇔{5|x|=0|x|−3√2y=12⇔{x=0y=−2√2
Vậy hệ có nghiệm duy nhất (x;y)=(0;−2√2) .
Câu 2: Số nghiệm của hệ phương trình {x2−2y2−x=4x2−2y2+2y=4 là:
- A
- B
- C
- D
{x2−2y2−x=4x2−2y2+2y=4⇔{x=−2yx2−2y2+2y=4
⇒(−2y)2−2y2+2y=4⇔y2+y−2=0⇔[y=1y=−2
Với y=1⇒x=−2
Với y=−2⇒x=4
Vậy hệ phương trình có 2 nghiệm là: (x;y)={(−2;1);(4;−2)}
Câu 3: Gọi (xo;yo) là nghiệm nguyên của hệ phương trình {2x−13y=x4x−y=1 . Giá trị của x2o+y2o là
- A
- B
- C
- D
Điều kiện: x≠0 .
Khi đó từ hệ phương trình đã cho suy ra
{6−xy=3x2y=4x−1⇔{6−x(4x−1)=3x2y=4x−1⇔{7x2−x−6=0y=4x−1⇔{[x=1x=−67y=4x−1⇔[{x=1y=3{x=−67y=−317
Vậy nghiệm nguyên của hệ phương trình là (xo;yo)=(1;3)
Ta có: x2o+y2o=12+32=10.
Câu 4: Cho hệ phương trình {x−2y=1√x+√2y+1=y+2 có nghiệm (xo;yo) với xo>1 . Tính xoyo .
- A
- B
- C
- D
{x−2y=1(1)√x+√2y+1=y+2(2) Điều kiện: x≥0;y≥−12
Từ (1) ⇒x=1+2y thế vào (2) ta được:
√1+2y+√2y+1=y+2⇔2√1+2y=y+2⇔{y≥−124(1+2y)=(y+2)2⇔{y≥−12y2−4y=0⇔[y=0y=4
Với y=0⇒x=1.
Với y=4⇒x=9.
Vì x>1 nên nghiệm của hệ thỏa mãn đề bài là: (xo;yo)=(9;4)
Ta có: xoyo=94 .
Câu 5: Hệ phương trình {(x−2y)2+4xy=yx2+4y2=2x với x<y có nghiệm là (xo;yo) . Tính xo−yo .
- A
- B
- C
- D
{(x−2y)2+4xy=yx2+4y2=2x⇔{x2+4y2=yx2+4y2=2x⇔{y=2xx2+4.(2x)2=2x⇔{y=2xx(17x−2)=0⇔[{x=0y=0{x=217y=417
Vì x<y nên (x;y)=(217;417) .
Vậy nghiệm của hệ phương trình thỏa mãn đề bài là (xo;yo)=(217;417) .
Ta có: xo−yo=217−417=−217
Câu 6: Số nghiệm của hệ phương trình {x+|y|=52x−|y|=4 là:
- A
- B
- C
- D
{x+|y|=52x−|y|=4⇔{3x=9|y|=5−x⇔{x=3|y|=2⇔[{x=3y=−2{x=3y=2
Vậy hệ phương trình có 2 nghiệm (x;y)={(3;−2),(3;2)} .
Câu 7: Hệ phương trình {x2−xy+y2=3x3−3(x+y)=1 với x<0 có nghiệm (xo;yo) . Tính |xo−yo| .
- A
- B
- C
- D
{x2−xy+y2=3(1)x3−3(x+y)=1(2)
Thế 3=x2−xy+y2 vào phương trình (2) ta được:
x3−(x2−xy+y2)(x+y)=1⇔x3−(x3−y3)=1⇔y3=1⇔y=1
Với y=1 thay vào phương trình (1) ta được:
x2−x=2⇔x2−x−2=0⇔[x=−1x=2
Vì x<0 nên nghiệm của hệ thỏa mãn đề bài là (xo;yo)=(−1;1)
Ta có: |xo−yo|=|−1−1|=2 .