Cường độ điện trường
Lý thuyết về Cường độ điện trường
+ Cường độ điện trường: Là đại lượng đặc trưng cho điện trường về khả năng tác dụng lực.
→E=→Fq⇒→F=q.→E
Đơn vị: E(V/m)
q>0 : →F cùng phương, cùng chiều với →E.
q<0 : →F cùng phương, ngược chiều với→E.
+ Véctơ cường độ điện trường →E do 1 điện tích điểm Q gây ra tại một điểm M cách Q một đoạn r có:
- Điểm đặt: Tại M.
- Phương: đường nối M và Q
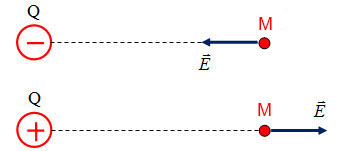
- Chiều: Hướng ra xa Q nếu Q>0 ; Hướng vào Q nếu Q<0
- Độ lớn:E=k|Q|ε.r2 ; k=9.109 (N.m2C2)
Trong môi trường không khí và chân không hằng số điện môi bằng 1.
+ Nguyên lí chồng chất điện trường: →E=→E1+→E2+.....→+En
+Biểu diễn:
Xét trường hợp tại điểm đang xét chỉ có 2 cường độ điện trường
+ →E=→E1+→E2
+ →E1↑↑→E2⇒E=E1+E2
+ →E1↑↓→E2⇒E=|E1−E2|
+ →E1⊥→E2⇒E=√E21+E22
+ (→E1,→E2)=α⇒E=√E21+E22+2E1E2cosα
Neáu E1=E2⇒E=2E1cosα2
Bài tập tự luyện có đáp án
Câu 1: Công thức nào sau đây đúng để tính cường độ điện trường của một điện tích điểm Q?
- A
- B
- C
- D
Công thức xác định cường độ điện trường của một điện tích điểm gây ra tại một điểm là
E=k|Q|εr2
Trong đó k=9.109N.m2/C2
Q là điện tích điểm đang xét
ε là hằng số điện mội của môi trường
r là khoảng cách từ điểm đang xét đến điện tích điểm Q.
Câu 2: Cho một điện tích điểm −Q đặt trong không khí. Véctơ cường độ điện trường tại một điểm mà nó gây ra có chiều
- A
- B
- C
- D
Véc tơ cường độ điện trường của điện tích điểm có chiếu hương về phía điện tích nếu Q < 0 và có chiều hướng ra xa điện tích nếu Q > 0
Câu 3: Đơn vị nào sau đây là đơn vị đo cường độ điện trường?
- A
- B
- C
- D
Đơn vị của cường độ điện trường là V/m.
Câu 4: Cho một điện tích điểm + Q đặt trong không khí. Véctơ cường độ điện trường tại một điểm mà nó gây ra có chiều
- A
- B
- C
- D
Véc tơ cường độ điện trường của điện tích điểm có chiếu hương về phía điện tích nếu Q < 0 và có chiều hướng ra xa điện tích nếu Q > 0
Câu 5: Véc tơ cường độ điện trường tại mỗi điểm có chiều
- A
- B
- C
- D
Nếu một điện tích q đặt trong điện trường →E thì sẽ chịu tác dụng của lực điện →F=q→E
Điện tích thử q>0 , do đó →F↑↑→E
Câu 6: Công thức xác định cường độ điện trường gây ra bởi điện tích Q < 0, tại một điểm trong chân không, cách điện tích Q một khoảng r là
- A
- B
- C
- D
Công thức xác định cường độ điện trường của một điện tích điểm gây ra tại một điểm là
E=k|Q|εr2.
Vì Q < 0 và được đặt trong môi trường chân không có ε = 1 nên công thức trên trở thành
E=−9.109Qr2.
Câu 7: Đối với các vật dẫn ở trạng thái cân bằng điện, véctơ cường độ điện trường trên mặt vật dẫn luôn
- A
- B
- C
- D
Đối với các vật dẫn ở trạng thái cân bằng điện, véctơ cường độ điện trường trên mặt vật dẫn luôn luôn có phương vuông góc với bề mặt vật dẫn và có chiều hướng ra ngoài.
Câu 8: Cường độ điện trường tại một điểm đặc trưng cho
- A
- B
- C
- D
Cường độ điện trường, kí hiệu là →E , là đại lượng đặc trưng cho điện trường về phương diện tác dụng lực của điện trường tại điểm đó.
Câu 9: Đặt các điện tích điểm q1,q2,q3 tại các điểm A, B, C trong một điện trường. Cường độ điện trường tại đó là E1,E2,E3. Lực điện tác dụng lên các điện tích đó là F1>F2>F3. Có thể rút ra kết luận nào dưới đây?
- A
- B
- C
- D
Ta có lực điện
Fi=qi.Ei với i = 1, 2, 3.
do ta không thể xác định được qi và Ei do đó không thể kết luận gì về Ei .
Câu 10: Độ lớn cường độ điện trường tại một điểm gây bởi một điện tích điểm không phụ thuộc vào
- A
- B
- C
- D
Công thức xác định cường độ điện trường do điện tích điểm Q gây ra tại một điểm
E=k|Q|εr2
Trong đó k=9.109N.m2/C2
Q là điện tích điểm đang xét
ε là hằng số điện mội của môi trường
r là khoảng cách từ điểm đang xét đến điện tích điểm Q.
Như vậy cường độ điện trường của một điện tích điểm tại một điện không phụ thuộc vào độ lớn điện tích thử.
Câu 11: Đại lượng nào dưới đây không liên quan đến độ lớn cường độ điện trường của một điện tích điểm Q tại một điểm đặt điện tích thử?
- A
- B
- C
- D
Ta có cường độ điện trường tổng quát
E=k|Q|εr2
ở đây có các đại lượng liên quan là điện tích Q ; khoảng cách r và hằng số điện môi ε.
Ta thấy điện tích thử q không có mặt trong biểu thức tính trên.
Xem thêm các bài tiếp theo bên dưới