Các công thức tính nhanh cực trị hàm bậc ba $y = ax^3 + bx^3 + cx + d$
Lý thuyết về Các công thức tính nhanh cực trị hàm bậc ba $y = ax^3 + bx^3 + cx + d$
Xét hàm số $y = ax^3 + bx^2 + cx + d\,\,(a \ne 0)$
- Hàm số không có cực trị (hay hàm số đơn điệu trên $\mathbb{R}$) khi $b^2 \le 3ac$.
- Hàm số có hai cực trị khi $b^2 > 3ac$.
- Đường thẳng đi qua hai điểm cực trị (nếu có) của đồ thị hàm số: $y = \left(\dfrac{2c}{3} - \dfrac{2b^2}{9a}\right)x + d - \dfrac{bc}{9a}$.
- Giả sử hai điểm cực trị $x_1, x_2$. Khi đó: $\left\{ \begin{array}{l} x_1 + x_2 = \dfrac{-2b}{3a}\\ x_1x_2 = \dfrac{c}{3a}\\ \left| {{x_1} - {x_2}} \right| = \dfrac{2}{{3\left| a \right|}}\sqrt {{b^2} - 3ac}\\ \end{array} \right.$.
- Gọi $x_1 < x_2$ là hai nghiệm của $y' = 0$.
- Khi $a > 0$ thì $x_1$ là điểm cực đại của hàm số, $x_2$ là điểm cực tiểu của hàm số.
- Khi $a < 0$ thì $x_1$ là điểm cực tiểu của hàm số, $x_2$ là điểm cực đại của hàm số.
Bài tập tự luyện có đáp án
Câu 1: Cho hàm số $ y=\dfrac{{ x ^ 3 }} 3 -m\dfrac{{ x ^ 2 }} 2 +\dfrac 1 3 $ đạt cực tiểu tại $ { x _ 0 }=2 $ khi
- A
- B
- C
- D
Ta có: $ y'={ x ^ 2 }-mx\Rightarrow y'\left( 2 \right)=4-2m=0\Leftrightarrow m=2 $
Khi đó $ y''\left( 2 \right)=2.2-2=2 > 0 $ . Do vậy với $ m=2 $ thì hàm số đạt cực tiểu tại $ x=2 $ .
Câu 2: Hàm số $ y=\dfrac{1}{3} { x ^ 3 }+m{ x ^ 2 }+\left( { m ^ 2 }+2m \right)x-1 $ có hai điểm cực trị khi và chỉ khi:
- A
- B
- C
- D
$ y'={ x ^ 2 }+2mx+{ m ^ 2 }+2m $
Hàm số có 2 điểm cực trị khi
$ \Delta ' > 0\Leftrightarrow { m ^ 2 }-\left( { m ^ 2 }+2m \right) > 0\Leftrightarrow m < 0 $
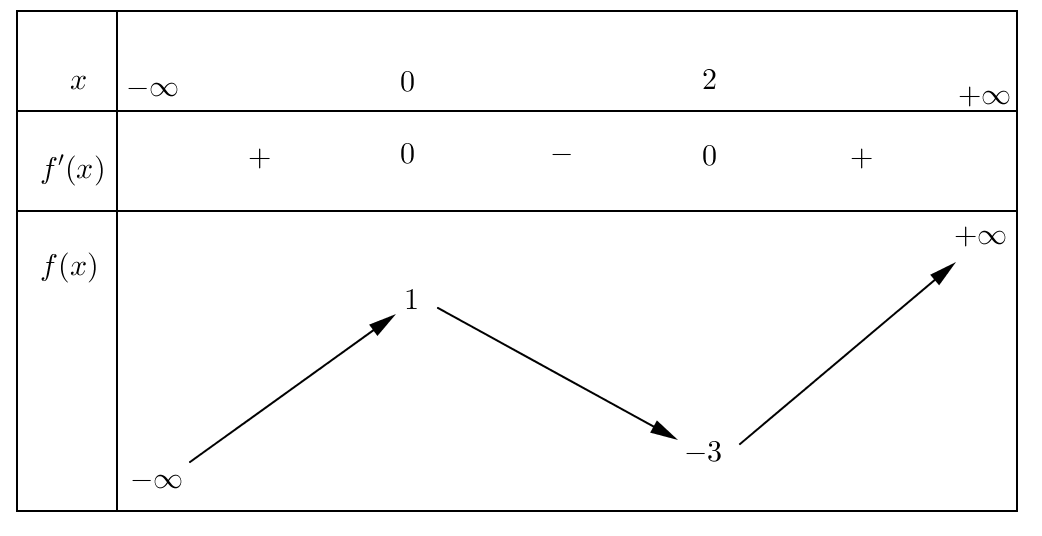
Câu 3: Cho hàm số $ y=f\left( x \right) $ liên tục trên $ \mathbb{R} $ và có bảng biến thiên như hình dưới đây:

Mệnh đề nào dưới đây đúng?

Mệnh đề nào dưới đây đúng?
- A
- B
- C
- D
Từ bảng biến thiên suy ra giá trị cực đại của hàm số bằng 1.
Câu 4: Tìm m để hàm số $ y={ x ^ 3 }-3m{ x ^ 2 }+3\left( { m ^ 2 }-1 \right)x+m $ đạt cực đại tại $ x=2 $
- A
- B
- C
- D
$ y'=3{{ x }^ 2 }-6m x +3{ m ^ 2 }-3;\,\,y''=6 x -6m $
\[\begin{gathered}
YCBT \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{}&{y'\left( 2 \right) = 0} \\
{}&{y''\left( 2 \right) < 0}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{}&{12 - 12m + 3{m^2} - 3 = 0} \\
{}&{12 - 6m < 0}
\end{array}} \right. \hfill \\
\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{}&{\left[ {\begin{array}{*{20}{l}}
{}&{m = 1} \\
{}&{m = 3}
\end{array}} \right.} \\
{}&{m > 2}
\end{array}} \right. \Leftrightarrow m = 3\ . \hfill \\
\end{gathered} \]
Câu 5: Hàm số $ y=\dfrac{1}{3} (m+1){ x ^ 3 }+2m{ x ^ 2 }+(3m+2)x+1 $ có cực đại, cực tiểu khi và chỉ khi.
- A
- B
- C
- D
$ y'=\left( m+1 \right){ x ^ 2 }+4mx+3m+2 $
Hàm số có cực đại cực tiểu khi
$ \begin{array}{l} & \left\{ \begin{array}{l} & m\ne -1 \\ & \Delta ' > 0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} & m\ne -1 \\ & 4{ m ^ 2 }-\left( 3m+2 \right)\left( m+1 \right) > 0 \\ \end{array} \right. \\ & \Leftrightarrow \left\{ \begin{array}{l} & m\ne -1 \\ & { m ^ 2 }-5m-2 > 0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} & \left[ \begin{array}{l} & m < \dfrac{5-\sqrt{33}} 2 \\ & m > \dfrac{5+\sqrt{33}} 2 \\ \end{array} \right. \\ & m\ne -1 \\ \end{array} \right. \\ \end{array} $
Câu 6: Cho hàm số $ y=-{ x ^ 3 }+2\left( m+1 \right){ x ^ 2 }+mx+3 $ . Giá trị của m để hàm số đạt cực tiểu tại điểm $ x=\dfrac{4}{3} $ là:
- A
- B
- C
- D
$ y'=-3{ x ^ 2 }+4\left( m+1 \right)x+m;\,\,y''=-6x+4m+4 $
Hàm số đạt cực tiểu tại điểm $ x=\dfrac{4}{3} $
$ \begin{array}{l} & \Leftrightarrow \left\{ \begin{array}{l} & y'\left( \dfrac{4}{3} \right)=0 \\ & y''\left( \dfrac{4}{3} \right) > 0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} & -3.{{\left( \dfrac{4}{3} \right)}^ 2 }+4\left( m+1 \right).\dfrac{4}{3} +m=0 \\ & -6.\dfrac{4}{3} +4m+4 > 0 \\ \end{array} \right. \\ & \Leftrightarrow \left\{ \begin{array}{l} & \dfrac{19m} 3 =0 \\ & 4m-4 > 0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} & m=0 \\ & m > 1 \\ \end{array} \right.\Leftrightarrow m\in \varnothing \\ \end{array} $
Câu 7: Cho hàm số $y=ax^3 + bx^2 + cx + d\,\,\,\left( a\ne 0 \right)$. Điều kiện để hàm số có cực trị trên khoảng $K$ là
- A
- B
- C
- D
Hàm bậc ba có cực trị trên khoảng K khi $y'=0$ có hai nghiệm phân biệt trên K hoặc $y'=0$ có hai nghiệm phân biệt trong đó có 1 nghiệm thuộc K.
Câu 8: Hàm số $ y=\left( m-3 \right){ x ^ 3 }-2m{ x ^ 2 }+3 $ không có cực trị khi
- A
- B
- C
- D
Ta có $ m=3\Rightarrow y=-6{ x ^ 2 }+3 $ hàm số có một điểm cực trị
Với $ m\ne 3\Rightarrow y'=3\left( m-3 \right){ x ^ 2 }-4mx=0\Leftrightarrow \left[ \begin{array}{l} & x=0 \\ & x=\dfrac{4m}{3(m-3)} \\ \end{array} \right. $
Hàm số không có cực trị $ \Leftrightarrow \dfrac{4m}{3(m-3)}=0\Leftrightarrow m=0 $ .
Câu 9: Giá trị của m để hàm số $ y=\dfrac{1}{3} { x ^ 3 }-m{ x ^ 2 }+({ m ^ 2 }-m+1)x+1 $ đạt cực đại tại điểm $ x=1 $ :
- A
- B
- C
- D
$ \begin{array}{l} & y'={ x ^ 2 }-2mx+{ m ^ 2 }-m+1 \\ & y''=2x-2m \\ \end{array} $
Hàm số đạt cực đại tại $ x=1 $
$ \begin{array}{l} & \Leftrightarrow \left\{ \begin{array}{l} & y'\left( 1 \right)=0 \\ & y''\left( 1 \right) < 0 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} & 1-2m+{ m ^ 2 }-m+1=0 \\ & 2-2m < 0 \\ \end{array} \right. \\ & \Leftrightarrow \left\{ \begin{array}{l} & \left[ \begin{array}{l} & m=1 \\ & m=2 \\ \end{array} \right. \\ & m > 1 \\ \end{array} \right.\Leftrightarrow m=2 \\ \end{array} $
Câu 10: Cho hàm số $ y=\dfrac{1}{3} { x ^ 3 }-m{ x ^ 2 }+\left( { m ^ 2 }-m-1 \right)x+2 $ . Tìm $ m $ để hàm số đạt cực đại tại $ x=-1 $
- A
- B
- C
- D
$ y'={ x ^ 2 }-2mx+{ m ^ 2 }-m-1;\,y''=2x-2m $
$ YCBT\Leftrightarrow \left\{ \begin{array}{l} & y'\left( -1 \right)=0 \\ & y''\left( -1 \right) < 0 \\ \end{array} \right.$
$\Leftrightarrow \left\{ \begin{array}{l} & 1+2m+{ m ^ 2 }-m-1=0 \\ & -2-2m < 0 \\ \end{array} \right.$
$\Leftrightarrow \left\{ \begin{array}{l} & m\left( m+1 \right)=0 \\ & m > -1 \\ \end{array} \right.$
$\Leftrightarrow m=0 $ .
Xem thêm các bài tiếp theo bên dưới