Phương trình dạng chứ dấu | |, chứa ẩn ở mẫu

$|2x-1|\,=\,|x+2|\Leftrightarrow \left[ \begin{array}{l} & 2x-1=x+2 \\ & 2x-1=-x-2 \end{array} \right.\Leftrightarrow \left[ \begin{array}{l} & x=3 \\ & x=-\dfrac{1}{3} \end{array} \right..$

Điều kiện: $x-1\ge 0\Leftrightarrow x\ge 1.$

Điều kiện: $\left\{ \begin{array}{l} & 1-x\ge 0 \\ & x+2\ne 0 \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} & x\le 1 \\ & x\ne -2 \end{array} \right..$

Điều kiện: $x\ge 2$ .

Khi đó: $\sqrt{x-2}+x=\sqrt{x-2}+3\Leftrightarrow x=3.$

Điều kiện $x\ne 0$ .

Phương trình  $\dfrac{2x-1}{x}=1\Leftrightarrow 2x-1=x\Leftrightarrow x=1$(Thỏa mãn).

Vậy nghiệm của phương trình là $x = 1$.

Điều kiện: $\left\{ \begin{array}{l} & x-2\ge 0 \\ & 2-x\ge 0 \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} & x\ge 2 \\ & x\le 2 \end{array} \right.\Leftrightarrow x=2.$

Với $x=2$ thay vào ta thấy $2=1$ (vô lý)

Vậy phương trình vô nghiệm.

Thay lần lượt các giá trị $x=1 ;x=2; x=-1;x=3$ ta thấy giá trị $x=2$ thỏa mãn phương trình đã cho.

Do đó $x=2$ là một nghiệm của phương trình.

Điều kiện: $x-1\ne 0\Leftrightarrow x\ne 1.$

$\dfrac{m{{x}^{2}}}{|x|-1}=m|x|+2m+1$ (1)

Điều kiện: $|x|\ne 1$

Khi đó từ phương trình (1) suy ra

$\begin{array}{l} & m{{x}^{2}}=\left( m|x|+2m+1 \right)\left( |x|-1 \right) \\ & \Leftrightarrow (m+1)|x|=2m+1\,\,\,\,\,\,\,\,\,\,\,\,(2) \end{array}$

+) Trường hợp 1: $m=-1$

$\Rightarrow \,\,\,(2)\Leftrightarrow 0|x|=-1$ (vô lý)

+) Trường hợp 2: $m\ne -1$

$\Rightarrow \,\,(2)\Leftrightarrow |x|=\dfrac{2m+1}{m+1}$ (3)

Ta có: $|x|\ne 1\,\Leftrightarrow \dfrac{2m+1}{m+1}\ne 1\Leftrightarrow \dfrac{m}{m+1}\ne 0\Leftrightarrow \left\{ \begin{array}{l} & m\ne -1 \\ & m\ne 0 \end{array} \right..$

Nếu $m=-\dfrac{1}{2}$ thì phương trình (3) có nghiệm duy nhất $x=0$ .

Nếu $\dfrac{2m+1}{m+1} < 0\Leftrightarrow -1 < m < -\dfrac{1}{2}$ $\Rightarrow \,$ (3) vô nghiệm.

Nếu $\dfrac{2m+1}{m+1} > 0\Leftrightarrow \left[ \begin{array}{l} & m > -\dfrac{1}{2} \\ & m < -1 \end{array} \right.$

$\Rightarrow$ Phương trình (3) có 2 nghiệm phân biệt $x=\pm \dfrac{2m+1}{m+1}$

Vậy $m\in \left( -\infty ;\,-1 \right)\cup \left( -\dfrac{1}{2};+\infty \right)\backslash \left\{ 0\, \right\}$ phương trình có 2 nghiệm phân biệt $x=\pm \dfrac{2m+1}{m+1}$

$\begin{array}{l} & \sqrt{{{x}^{2}}-x+1-3{{m}^{2}}}=x-m \\ & \Leftrightarrow \left\{ \begin{array}{l} & x\ge m \\ & {{x}^{2}}-x+1-3{{m}^{2}}={{(x-m)}^{2}} \end{array} \right. \\ & \Leftrightarrow \left\{ \begin{array}{l} & x\ge m \\ & (2m-1)x=4{{m}^{2}}-1\,\,\,(1) \end{array} \right. \end{array}$

Với $m=\dfrac{1}{2}$ thì $(1)\Leftrightarrow 0x=0$ (luôn đúng) $\Rightarrow$ (1) có vô số nghiệm.

Với $m\ne \dfrac{1}{2}$ thì (1) có nghiệm duy nhất $x=2m+1$

Ta có: $x=2m+1\ge m\Leftrightarrow m\ge -1$

Vậy với $m\ge -1\,;\,m\ne \dfrac{1}{2}$ thì phương trình có nghiệm duy nhất $x=2m+1$ .

$\dfrac{{{x}^{2}}-4}{{{(x-2)}^{2}}}=\dfrac{x+1}{x-m}$ (1).

Điều kiện: $x\ne 2\,;\,x\ne m$ .

Khi đó:

$\begin{array}{l} & \dfrac{x+2}{x-2}=\dfrac{x+1}{x-m} \\ & \Leftrightarrow (x+2)(x-m)=(x+1)(x-2) \\ & \Leftrightarrow x(3-m)=2m-2\,\,\,\,\,(2) \end{array}$

Với $m=3$ thay vào (2) ta được: $0x=4$ (vô lý).

Với $m\ne 3$ $\Rightarrow$ Phương trình (2) có nghiệm duy nhất $x=\dfrac{2m-2}{3-m}$

$x\ne 2\Leftrightarrow \dfrac{2m-2}{3-m}\ne 2\Leftrightarrow \left\{ \begin{array}{l} & m\ne 2 \\ & m\ne 3 \end{array} \right.$ .

$x\ne m\Leftrightarrow \dfrac{2m-2}{3-m}\ne m\Leftrightarrow \dfrac{{{m}^{2}}-m-2}{3-m}\ne 0\Leftrightarrow \left\{ \begin{array}{l} & m\ne -1 \\ & m\ne 2 \\ & m\ne 3 \end{array} \right.$ .

Do đó với $m\ne -1;,m\ne 2\,;\,m\ne 3$ thì phương trình có nghiệm duy nhất $x=\dfrac{2m-2}{3-m}$ .

$x < -2\Leftrightarrow \dfrac{2m-2}{3-m} < -2\Leftrightarrow \dfrac{4}{3-m} < 0\Leftrightarrow m > 3$

Vậy $m\in (3;+\infty )$ thỏa mãn đề bài.

$\begin{array}{l} & \sqrt{4{{x}^{2}}-4mx+{{m}^{2}}}=2-x \\ & \Leftrightarrow \sqrt{{{(2x-m)}^{2}}}=2-x \\ & \Leftrightarrow |2x-m|\,=2-x \\ & \Leftrightarrow \left[ \begin{matrix} \left\{ \begin{array}{l} & x\le 2 \\ & 2x-m=2-x \end{array} \right. \\ \left\{ \begin{array}{l} & x\le 2 \\ & 2x-m=x-2 \end{array} \right. \\ \end{matrix} \right.\Leftrightarrow \left[ \begin{array}{l} & \left\{ \begin{array}{l} & x\le 2 \\ & x=\dfrac{m+2}{3} \end{array} \right. \\ & \left\{ \begin{array}{l} & x\le 2 \\ & x=m-2 \end{array} \right. \end{array} \right. \end{array}$

+) $x=\dfrac{m+2}{3}\le 2\Leftrightarrow m\le 4$

+) $x=m-2\le 2\Leftrightarrow m\le 4$

Vậy $m\le 4$ phương trình có nghiệm: $x=\dfrac{m+2}{3}\,;\,x=m-2$ .

$\sqrt{x-2\sqrt{x-1}}+\sqrt{x+3-4\sqrt{x-1}}=m$ (1)

Điều kiện: $x\ge 1$ .

$\begin{array}{l} & (1)\Leftrightarrow \sqrt{{{\left( \sqrt{x-1}-1 \right)}^{2}}}+\sqrt{{{\left( \sqrt{x-1}-2 \right)}^{2}}}=m \\ & \Leftrightarrow \left| \sqrt{x-1}-1 \right|+\left| \sqrt{x-1}-2 \right|=m \end{array}$

Đặt $t=\sqrt{x-1}\,\,\,(t\ge 0)$ ta có phương trình: $|t-1|+|t-2|=m$ (2)

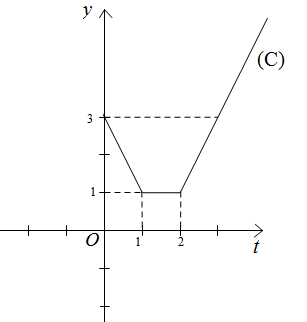
Vẽ đồ thị hàm số: $y=f(t)=|t-1|+|t-2|\,\,\,$ (C) với $t\ge 0$.

Ta có: $f(t)=\left\{ \begin{array}{lll} 2t-3 & khi & t > 2 \\ 1\ & khi\ & 1\le t\le 2 \\ 3-2t & khi & 0\le t < 1 \end{array} \right.$

Số nghiệm của phương trình (2) là số giao điểm của đồ thị hàm số (C) với đường thẳng $y=m$ .

Do đó, để phương trình có 2 nghiệm phân biệt thì $1 < m\le 3$ .

$|1-x|+|x|=m-1$ (1)

Ta thấy nếu ${{x}_{0}}$ là nghiệm của (1) thì $(1-{{x}_{0}})$ cũng là nghiệm của (1).

Do đó (1) có nghiệm duy nhất $\Leftrightarrow {{x}_{0}}=1-{{x}_{0}}\Leftrightarrow {{x}_{0}}=\dfrac{1}{2}.$

Thay ${{x}_{0}}=\dfrac{1}{2}$ vào (1) ta được: $m-1=1\Leftrightarrow m=2.$

Với $m=2$ phương trình (1) trở thành: $|1-x|+|x|=1$ (2)

Giải phương trình (2) ta có tập nghiệm $S = {\rm{ }}\left\{ {0;1} \right\}$ .

Vậy không có giá trị nào của $m$ để phương trình có nghiệm duy nhất.

$\dfrac{2mx-m}{\sqrt{x-1}}+\sqrt{x-1}=\dfrac{2(x+m)-1}{\sqrt{x-1}}$ (1)

Điều kiện: $x > 1$

Từ phương trình (1) suy ra:

$\begin{array}{l} & 2mx-m+x-1=2x+2m-1 \\ & \Leftrightarrow (2m-1)x=3m\,\,\,\,\,\,\,\,\,\,(2) \end{array}$

Với $m=\dfrac{1}{2}$ $\Rightarrow \,\,\,(2)\Leftrightarrow 0x=\dfrac{3}{2}$ (vô lý)

Với $m\ne \dfrac{1}{2}\,\,$ $\Rightarrow$ (2) có nghiệm duy nhất $x=\dfrac{3m}{2m-1}$

Để phương trình đã cho có nghiệm thỏa mãn $x < 2$ thì

$1 < \dfrac{3m}{2m-1} < 2\Leftrightarrow \left\{ \begin{array}{l} & \dfrac{m+1}{2m-1} > 0 \\ & \dfrac{2-m}{2m-1} < 0 \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} & \left[ \begin{array}{l} & m > \dfrac{1}{2} \\ & m < -1 \end{array} \right. \\ & \left[ \begin{array}{l} & m > 2 \\ & m < \dfrac{1}{2} \end{array} \right. \end{array} \right.\Leftrightarrow \left[ \begin{array}{l} & m < -1 \\ & m > 2 \end{array} \right.$ .

$\begin{array}{l} & 4x+|2x-m|=2+3x\Leftrightarrow |2x-m|=2-x \\ & \Leftrightarrow \left[ \begin{array}{l} & \left\{ \begin{array}{l} & 2-x\ge 0 \\ & 2x-m=2-x \end{array} \right. \\ & \left\{ \begin{array}{l} & 2-x\ge 0 \\ & 2x-m=x-2 \end{array} \right. \end{array} \right.\Leftrightarrow \left[ \begin{array}{l} & \left\{ \begin{array}{l} & x\le 2 \\ & x=\dfrac{m+2}{3} \end{array} \right. \\ & \left\{ \begin{array}{l} & x\le 2 \\ & x=m-2 \end{array} \right. \end{array} \right. \end{array}$

+) $\dfrac{m+2}{3}\le 2\Leftrightarrow m\le 4.$

+) $m-2\le 2\Leftrightarrow m\le 4.$

Vậy $m\le 4$ phương trình có nghiệm: $x=\dfrac{m+2}{3}\,;\,x=m-2$ .

$m > 4$ phương trình vô nghiệm.

$\begin{array}{l} & |mx-2|=|x+2m| \\ & \Leftrightarrow \left[ \begin{array}{l} & mx-2=x+2m \\ & mx-2=-x-2m \end{array} \right. \\ & \Leftrightarrow \left[ \begin{array}{l} & (m-1)x=2m+2\,\,\,(1) \\ & (m+1)x=2-2m\,\,\,\,(2) \end{array} \right. \end{array}$

+) Xét phương trình (1).

Với $m=1\,\,\Rightarrow \,\,0x=4$ (vô lý) $\Rightarrow$ (1) vô nghiệm.

Với $m\ne 1\,\,\,\Rightarrow$ (1) có nghiệm $x=\dfrac{2m+2}{m-1}$ .

+) Xét phương trình (2).

Với $m=-1\,\,\Rightarrow \,\,0x=4$ (vô lý) $\Rightarrow$ (2) vô nghiệm.

Với $m\ne -1\,\,\,\Rightarrow$ (2) có nghiệm $x=\dfrac{2-2m}{m+1}$ .

Ta thấy $m=1\,\,\Rightarrow$ (2) có nghiệm $x=0$

$m=-1\,\,\Rightarrow$ (1) có nghiệm $x=0$

Vậy $m\ne \pm 1$ $\Rightarrow$ Phương trình đã cho có 2 nghiệm ${{x}_{1}}=\dfrac{2m+2}{m-1}\,;\,{{x}_{2}}=\dfrac{2-2m}{m+1}$ .

$m=1\,\,\Rightarrow$ Phương trình có nghiệm $x=0$ .

$m=-1\,\,\Rightarrow$ Phương trình có nghiệm $x=0$ .

$\dfrac{{{x}^{2}}+(m-1)x-1}{\sqrt{x-2}}=\sqrt{x-2}\left( x-{{m}^{2}} \right)$ (1)

Điều kiện: $x > 2$

Khi đó từ phương trình (1) suy ra

$\begin{array}{l} & {{x}^{2}}+(m-1)x-1=(x-2)(x-{{m}^{2}}) \\ & \Leftrightarrow {{x}^{2}}+(m-1)x-1={{x}^{2}}-{{m}^{2}}x-2x+2{{m}^{2}} \\ & \Leftrightarrow \left( {{m}^{2}}+m+1 \right)x=2{{m}^{2}}+1 \\ & \Leftrightarrow x=\dfrac{2{{m}^{2}}+1}{{{m}^{2}}+m+1} \end{array}$

$\begin{array}{l} & x > 2\Leftrightarrow \dfrac{2{{m}^{2}}+1}{{{m}^{2}}+m+1} > 2 \\ & \Leftrightarrow \dfrac{-2m-1}{{{m}^{2}}+m+1} > 0 \\ & \Leftrightarrow -2m-1 > 0 \\ & \Leftrightarrow m < -\dfrac{1}{2} \end{array}$