Trong tất cả các hình chóp tứ giác đều có $\large d=\sqrt{3}$ là khoản

MỤC LỤC
Câu hỏi:
Trong tất cả các hình chóp tứ giác đều có $\large d=\sqrt{3}$ là khoảng cách giữa hai đường thẳng chéo nhau gồm một đường thẳng chứa một đường chéo của đáy và đường thẳng còn lại chứa một cạnh bên hình chóp. Thể tích nhỏ nhất của khối chóp bằng
Đáp án án đúng là: B
Lời giải chi tiết:
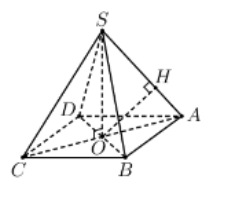
Xét hình chóp tứ giác đều $\large S.ABCD$
Đặt $\large AB=x,SO=h\longrightarrow V_{S.ABCD}=\frac{1}{3}hx^{2}$. Ta cần đánh giá $\large \frac{1}{3}hx^{2} \geq$ hằng số
Ta tính được $\large OA=\frac{x}{\sqrt{2}}$ nên theo giả thiết ta có
$\large\frac{1}{OH^{2}}=\frac{1}{SO^{2}}+\frac{1}{OA^{2}} \Leftrightarrow \frac{1}{d^{2}}=\frac{1}{h^{2}}+\frac{2}{x^{2}}$
$\large\Leftrightarrow \frac{1}{3}=\frac{1}{h^{2}}+\frac{2}{x^{2}}=\frac{1}{h^{2}}+\frac{1}{x^{2}}+\frac{1}{x^{2}}\underset{AM-OM}{\geq }3 \sqrt[3]{\frac{1}{h^{2}} \cdot \frac{1}{x^{4}}} \Leftrightarrow h x^{2} \geq 27$
Dấu "=" xảy ra $\large\Leftrightarrow x=h=3$. Khi đó $\large V_{min}=9$
Đáp án B
Xem thêm các bài tiếp theo bên dưới
- Cho một tấm nhôm hình chữ nhật có kích thước 80cmx50cm. Người ta cắt ở
- Cho tứ diện $\large ABCD$ có $\large S_{\bigtriangleup ABC}=4cm^{2},S_
- Cho hình chóp $\large S.ABC$ có đáy là tam giác với $\large AB=AC=5a,B
- Một người xây nhà xưởng hình hộp chữ nhật có diện tích sàn là $\large
- Cho hình chóp tứ giác đều $\large S.ABCD$ có cạnh đáy bằng $\large a$,